练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    用长度为24m、的材料围一个矩形场地，中间有两道隔墙，要使矩形的面积最大，则隔墙的长度应为多少？为什么？
    考点：基本不等式在最值问题中的应用
    专题：应用题,函数的性质及应用
    分析：若设矩形场地的宽为x，则长为
    24-4x
    2
    ，其面积为S=
    24-4x
    2
    •x，整理得x的二次函数，能求出函数的最值以及对应的x的值．
    解答： 解：如图所示，设矩形场地的宽为x，则长为
    24-4x
    2
    ，其面积为：
    S=
    24-4x
    2
    •x=12x-2x2=-2（x2-6x+9）+18=-2（x-3）2+18
    当x=3时，S有最大值，为18；
    所以隔墙宽应为3．
    点评：本题借助于矩形的周长与面积，考查了二次函数的最值问题，是基础题目．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    2008年5月18日某爱心人士为一位孤儿去银行存款a元，存的是一年定期储蓄；2009年5月18日他将到期存款的本息一起取出，再加a元后，还存一年的定期储蓄，此后每年5月18日都如此；假设银行一年定期储蓄的年利率r不变，直到2015年5月18日这位孤儿准备上大学时，他将所有的存款和利息全部取出并且资助给这位孤儿，取出的钱数共为（　　）
    A、a（1+r）7元
    B、a[（1+r）7+（1+r）]元
    C、
    a
    r
    [（1+r）7-r]元
    D、
    a
    r
    [（1+r）8-（1+r）]元

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    等差数列{an}各项均为正数，求证：
    1
    		a1
    +
    		a2
    +
    1
    		a2
    +
    		a3
    +…+
    1
    		an-1
    +
    		an
    =
    n-1
    		an
    +
    		a1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    把3个不同的礼物（A，B，C）分给2个人（甲，乙），有几种分法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一几何体的正视图和侧视图是边长为2的等边三角形，俯视图是直径为2的圆，则此几何体的表面积为（　　）
    A、4π+2
    		3
    B、2π+2
    		3
    C、3π
    D、2π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知Z=
    2
    x2
    +
    2y
    x
    +7    ，若x2+y2=2，求Z的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    =（6，2），
    b
    =（-4，
    1
    2
    ），过点A（3，-1）且与向量
    a
    +2
    b
    平行的直线l的方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知y=Asin（ωx+φ），（A＞0，ω＞0，-π＜φ＜π）的图象过点P（
    π
    12
    ，0），图象上与点P最近的一个顶点是Q（
    π
    3
    ，5）．
    （1）求函数f（x）≤0，x的取值范围．
    （2）求f（x）的对称中心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

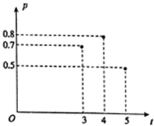    加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”，在特定条件下，可食用率p与加工时间t（单位：分钟）满足下列某函数关系：①p=at+b②p=alogbt③p=at2+bt+c（a，b，c是常数），如图记录了三次实验的数据，
    （1）根据这三次实验数据，请选用合适的函数模型，并说明理由
    （2）利用你选取的函数，求出最佳的加工时间．

    查看答案和解析>>

    同步练习册答案