
已知三次函数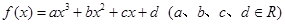 为奇函数,且在点
为奇函数,且在点 的切线方程为
的切线方程为
(1)求函数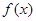 的表达式;
的表达式;
(2)已知数列 的各项都是正数,且对于
的各项都是正数,且对于 ,都有
,都有 ,求数列
,求数列 的首项
的首项 和通项公式;
和通项公式;
(3)在(2)的条件下,若数列 满足
满足 ,求数列
,求数列 的最小值.
的最小值.
(1) (2)
(2)
(3)①若 时, 数列
时, 数列 的最小值为当
的最小值为当 时,
时,
②若 时, 数列
时, 数列 的最小值为, 当
的最小值为, 当 时或
时或

③若 时, 数列
时, 数列 的最小值为,当
的最小值为,当 时,
时,
④若 时,数列
时,数列 的最小值为,当
的最小值为,当 时
时
解析试题分析:解:(1) ∵ 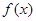 为奇函数,
为奇函数,  ,
,
即

 3分
3分 ,又因为在点
,又因为在点 的切线方程为
的切线方程为
 ,
, 4分
4分
(2)由题意可知: ....
....

 +
+
所以 ①
①
由①式可得 5分
5分
当 ,
, ②
②
由①-②可得:
∵ 为正数数列
为正数数列 ..③ 6分
..③ 6分 ④
④
由③-④可得:
∵ >0,
>0, ,
, 是以首项为1,公差为1的等差数列, 8分
是以首项为1,公差为1的等差数列, 8分 9分
9分
(注意:学生可能通过列举然后猜测出 ,扣2分,即得7分)
,扣2分,即得7分)
(3) ∵
 ,
,
令 ,
, 10分
10分
(1)当 时,数列
时,数列 的最小值为当
的最小值为当 时,
时, 11分
11分
(2)当 时
时
①若 时, 数列
时, 数列 的最小值为当
的最小值为当 时,
时,
②若 时, 数列
时, 数列 的最小值为, 当
的最小值为, 当 时或
时或

③若 时, 数列
时, 数列 的最小值为,当
的最小值为,当 时,
时,
④若 时,数列
时,数列


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
对于无穷数列 和函数
和函数 ,若
,若 ,则称
,则称 是数列
是数列 的母函数.
的母函数.
(Ⅰ)定义在 上的函数
上的函数 满足:对任意
满足:对任意 ,都有
,都有 ,且
,且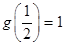 ;又数列
;又数列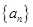 满足:
满足: .
.
求证:(1) 是数列
是数列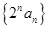 的母函数;
的母函数;
(2)求数列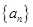 的前项
的前项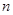 和
和 .
.
(Ⅱ)已知 是数列
是数列 的母函数,且
的母函数,且 .若数列
.若数列 的前
的前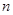 项和为
项和为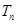 ,求证:
,求证: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com