
| A. | y2=2x-12 | B. | y2=2x+4 | C. | y2=x+1 | D. | y2=x-3 |
分析 根据条件可设$A(\frac{{{y}_{1}}^{2}}{2},{y}_{1}),B(\frac{{{y}_{2}}^{2}}{2},{y}_{2}),M(x,y)$,从而由$\overrightarrow{OA}•\overrightarrow{OB}=3$得出$\frac{({y}_{1}{y}_{2})^{2}}{4}+{y}_{1}{y}_{2}=3$,从而可解出y1y2=-6,从而有$\left\{\begin{array}{l}{x=(\frac{{y}_{1}+{y}_{2}}{2})+3}\\{y=\frac{{y}_{1}+{y}_{2}}{2}}\end{array}\right.$,这样即可求出点M的坐标满足的方程.
解答 解:设$A(\frac{{{y}_{1}}^{2}}{2},{y}_{1}),B(\frac{{{y}_{2}}^{2}}{2},{y}_{2})$,M(x,y),则:
$\overrightarrow{OA}•\overrightarrow{OB}=\frac{{{y}_{1}}^{2}{{y}_{2}}^{2}}{4}+{y}_{1}{y}_{2}=3$;
即$({y}_{1}{y}_{2})^{2}+4{y}_{1}{y}_{2}-12=0$;
解得y1y2=-6,或2;
∵y1,y2异号;
∴y1y2=-6;
∴$\left\{\begin{array}{l}{x=\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{4}=\frac{({y}_{1}+{y}_{2})^{2}}{4}+3}\\{y=\frac{{y}_{1}+{y}_{2}}{2}}\end{array}\right.$;
∴x=y2+3,即y2=x-3.
故选:D.
点评 考查抛物线上点的坐标的设法,数量积的坐标运算,一元二次方程的解法,以及中点坐标公式,完全平方公式的运用.


科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是$\frac{\sqrt{3}}{6}$,该四棱锥的最长棱的棱长为$\sqrt{2}$.
一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是$\frac{\sqrt{3}}{6}$,该四棱锥的最长棱的棱长为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 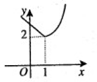 | B. |  | C. | 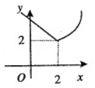 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com