
已知函数y=f(x)是定义在R上的增函数,函数y=f(x-1)的图象关于点(1,0)对称,若对任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )
A.(3,7) B.(9,25)
C.(13,49) D.(9,49)
C
[解析] 因为函数y=f(x-1)的图象关于点(1,0)对称,所以函数y=f(x)的图象关于原点对称,所以函数y=f(x)为R上的奇函数,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,即为f(x2-6x+21)<-f(y2-8y)=f(8y-y2)恒成立,因为函数y=f(x)是定义在R上的增函数,所以x2-6x+21<8y-y2恒成立,即x2+y2-6x-8y+21<0恒成立,即点(x,y)恒在圆(x-3)2+(y-4)2=4内,当x>3时,x2+y2表示半圆(x-3)2+(y-4)2=4(x>3)上的点到原点的距离的平方,所以最大为( +2)2=49,最小为点(3,2)到原点的距离的平方,即为32+22=13,所以x2+y2的取值范围是(13,49).
+2)2=49,最小为点(3,2)到原点的距离的平方,即为32+22=13,所以x2+y2的取值范围是(13,49).


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
设Sn表示数列{an}的前n项和.
(1)若{an}是等差数列,推导Sn的计算公式;
(2)若a1=1,q≠0,且对所有正整数n,有Sn=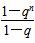 .判断{an}是否为等比数列,并证明你的结论.
.判断{an}是否为等比数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:
2
22 23
24 25 26
27 28 29 210
……
记M(s,t)表示该数阵中第s行的第t个数,则M(11,2)对应的数是________(用2n的形式表示,n∈N).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义域为R的偶函数f(x)在(-∞,0]上是减函数,且f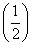 =2,则不等式f(log4x)>2的解集为( )
=2,则不等式f(log4x)>2的解集为( )
A.(0,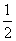 )∪(2,+∞) B.(2,+∞)
)∪(2,+∞) B.(2,+∞)
C.(0,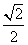 )∪(
)∪(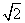 ,+∞) D.(0,
,+∞) D.(0,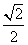 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
设二次函数f(x)=ax2+bx+c,函数F(x)=f(x)-x的两个零点为m,n(m<n).
(1)若m=-1,n=2,求不等式F(x)>0的解集;
(2)若a>0,且0<x<m<n<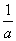 ,比较f(x)与m的大小.
,比较f(x)与m的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
经过抛物线y=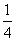 x2的焦点和双曲线
x2的焦点和双曲线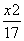 -
-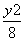 =1的右焦点的直线方程为( )
=1的右焦点的直线方程为( )
A.x+48y-3=0 B.x+80y-5=0
C.x+3y-3=0 D.x+5y-5=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com