
设Sn表示数列{an}的前n项和.
(1)若{an}是等差数列,推导Sn的计算公式;
(2)若a1=1,q≠0,且对所有正整数n,有Sn=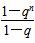 .判断{an}是否为等比数列,并证明你的结论.
.判断{an}是否为等比数列,并证明你的结论.
(1)方法一:设{an}的公差为d,则
Sn=a1+a2+…+an=a1+(a1+d)+…+[a1+(n-1)d],
又Sn=an+an-1+…+a1
=[a1+(n-1)d]+[a1+(n-2)d]+…+a1,
∴2Sn=[2a1+(n-1)d]+[2a1+(n-1)d]+…+[2a1+(n-1)d]=2na1+n(n-1)d,
∴Sn=na1+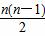 d.
d.
方法二:设{an}的公差为d,则
Sn=a1+a2+…+an=a1+(a1+d)+…+[a1+(n-1)d],
又Sn=an+(an-d)+…+[an-(n-1)d],两式相加得2Sn=n(a1+an),
∴Sn= .
.
(2){an}是等比数列,证明如下:∵Sn=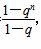 ,
,
∴an+1=Sn+1-Sn=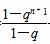 -
-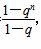 =
=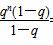 =qn.
=qn.
∵a1=1,q≠0,∴当n≥1时,有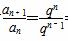 =q,
=q,
因此,{an}是首项为1且公比为q的等比数列.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
将正偶数按下表排成5列:
|
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 |
| 第1行 |
| 2 | 4 | 6 | 8 |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 |
| 18 | 20 | 22 | 24 |
| …… |
| …… | 28 | 26 |
那么2014应该在第________行第________列.
查看答案和解析>>
科目:高中数学 来源: 题型:
三个实数a,b,c成等比数列,且a+b+c=3,则b的取值范围是( )
A.[-1,0) B.(0,1]
C.[-1,0)∪(0,3] D.[-3,0)∪(0,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
将正偶数集合{2,4,6,…}从小到大按第n组有2n个偶数进行分组如下:
第一组 第二组 第三组 …
{2,4} {6,8,10,12} {14,16,18,20,22,24,26,28} …
则2014位于( )
A.第7组 B.第8组
C.第9组 D.第10组
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等比数列{an}的各项均为正数,公比q≠1,设P=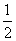 (log0.5a5+log0.5a7),Q=log0.5
(log0.5a5+log0.5a7),Q=log0.5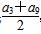 ,P与Q的大小关系是( )
,P与Q的大小关系是( )
A.P≥Q B.P<Q
C.P≤Q D.P>Q
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}中,a1=2,其前n项和Sn满足Sn+1-Sn=2n+1(n∈N*).
(1)求数列{an}的通项公式an以及前n项和Sn;
(2)令bn=2log2an+1,求数列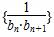 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数y=f(x)是定义在R上的增函数,函数y=f(x-1)的图象关于点(1,0)对称,若对任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )
A.(3,7) B.(9,25)
C.(13,49) D.(9,49)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com