练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    将正偶数集合{2,4,6，…}从小到大按第n组有2n个偶数进行分组如下：

    第一组　第二组　　　　　　第三组　　　 　　　…

    {2,4}　{6,8,10,12}　{14,16,18,20,22,24,26,28}　…

    则2014位于(　　)

    A．第7组                                                     B．第8组

    C．第9组                                                     D．第10组


    C

    [解析]　前n组共有2＋4＋8＋…＋2n＝＝2n＋1－2个数．

    由an＝2n＝2014知，n＝1007，∴2014为第1007个偶数，

    ∵29＝512,210＝1024，故前8组共有510个数，前9组共有1022个数，即2014在第9组．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在平行四边形ABCD中，∠BAD＝60°，AD＝2AB，若P是平面ABCD内一点，且满足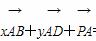＝0(x，y∈R)，则当点P在以A为圆心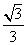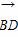，||为半径的圆上时，实数x，y应满足关系式为(　　)

    A．4x2＋y2＋2xy＝1                                       B．4x2＋y2－2xy＝1

    C．x2＋4y2－2xy＝1                                       D．x2＋4y2＋2xy＝1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn表示等差数列{an}的前n项和，已知＝，那么等于(　　)

    A.  B.  C.  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的首项a1＝1，且满足an＋1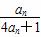＝ (n∈N*)．

    (1)设bn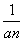＝，求证：数列{bn}是等差数列，并求数列{an}的通项公式；

    (2)设cn＝bn·2n，求数列{cn}的前n项和Sn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项的和Sn满足Sn＝2n－1(n∈N*)，则数列{a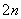}的前n项的和为(　　)

    A．4n－1                                                       B.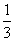(4n－1)

    C.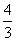(4n－1)                                                   D．(2n－1)2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn表示数列{an}的前n项和．

    (1)若{an}是等差数列，推导Sn的计算公式；

    (2)若a1＝1，q≠0，且对所有正整数n，有Sn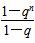＝.判断{an}是否为等比数列，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某程序框图如图所示，该程序运行后输出的k的值是(　　)

    A．4  B．5  C．6  D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知{an}为等差数列，{bn}为正项等比数列，公式q≠1，若a1＝b1，a11＝b11，则(　　)

    A．a6＝b6                                                     B．a6>b6

    C．a6<b6                                                       D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若关于x的不等式m(x－1)>x2－x的解集为{x|1<x<2}，则实数m的值为________．

    查看答案和解析>>

    同步练习册答案