
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
分析 利用数量积和三角公式得出$\overrightarrow{AB}$$•\overrightarrow{BC}$=2cos18°cos63°+2sin18°sin63°=2cos(18°-63°)=2sin45=$\sqrt{2}$>0,判断向量$\overrightarrow{AB}$,$\overrightarrow{BC}$的夹角,即可得出∠B为钝角.
解答 解:∵$\overrightarrow{AB}$=(cos18°,cos72°),$\overrightarrow{BC}$=(2cos63°,2cos27°),
∴$\overrightarrow{AB}$=(cos18°,sin18°),$\overrightarrow{BC}$=(2cos63°,2sin63°),
∵$\overrightarrow{AB}$$•\overrightarrow{BC}$=2cos18°cos63°+2sin18°sin63°=2cos(18°-63°)=2sin45=$\sqrt{2}$>0,
∴向量$\overrightarrow{AB}$,$\overrightarrow{BC}$的夹角为锐角,
∴∠B为钝角,
∴△ABC是钝角三角形.
点评 本题考查了平面向量与三角形的关系,数量积的运用判断三角形的形状,属于中档题,关键是判断三角形的夹角与向量的夹角的关系.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
| P(X2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
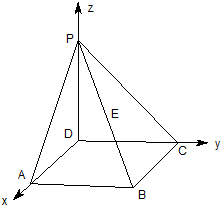 PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )
PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )| A. | (1,1,2) | B. | (2,2,1) | C. | (1,1,1) | D. | $(1\;,\;1\;,\;\frac{1}{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com