
| A. |  | B. |  | C. | 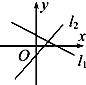 | D. |  |
分析 把二直线的方程化为斜截式,先假设其中一条直线正确,看另一条直线的斜率和截距是否符合即可.
解答 解:直线l1的方程是ax-y+b=0,可化为y=ax+b,l2的方程是bx+y-a=0,可化为y=-bx+a(ab≠0).
假设A选项直线l1正确:即斜率a>0,在y轴上的截距b<0.而直线l2的斜率-b>0,与图中符合,故A正确.
假设B选项直线l1正确:即斜率a>0,在y轴上的截距b>0.则图中直线l2的斜率为正,直线l2的-b<0,不满足题目条件,故B不正确.
假设C选项直线l1正确:即斜率a<0,在y轴上的截距b>0.则图中直线l2的斜率-b<0,与直线l2的斜率矛盾.故C不正确.
假设D选项直线l1正确:即斜率a<0,在y轴上的截距b<0.则图中直线l2的斜率满足题意,在y轴上的截距皆小于0,与解析式y=-bx+a(ab≠0,a≠b)中的焦距不相符.所以不正确.
综上可知只有A正确.
故选:A.
点评 本题考查函数的图象的判断,正确理解直线的斜率和截距是解题的关键.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{6}{7}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1的相关指数R2为0.50 | B. | 模型2的相关指数R2为0.80 | ||
| C. | 模型3的相关指数R2为0.90 | D. | 模型4的相关指数R2为0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2+3x=0 | B. | x2-y2-3x=0 | C. | x2-y2+3x=0 | D. | x2+y2-3x=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com