
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
| 2π |
| ω |
| π |
| 3 |
| π |
| 3 |
| 2π |
| ω |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 3 |
| 5π |
| 12 |


科目:高中数学 来源: 题型:
| A、m≤-1 | B、m≥1 |
| C、0≤m≤1 | D、-1≤m≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
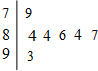 如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )| A、85,84 |
| B、84,85 |
| C、86,84 |
| D、84,86 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| A、最小正周期为π的偶函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为π的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 区间 | [17,19) | [19,21) | [21,23) | [23,25) | [25,27) | [27,29) | [29,31) | [31,33] |
| 频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
| A、42% | B、58% |
| C、40% | D、16% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com