练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知四棱锥P－ABCD的底面为直角梯形，AB∥DC，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC＝2AB＝4.

    (1)根据已经给出的此四棱锥的主视图，画出其俯视图和左视图．

    (2)证明：平面PAD⊥平面PCD.


    [解析]　(1)

    (2)∵PA⊥平面ABCD，PA平面PAD，

    ∴平面PAD⊥平面ABCD，

    又平面PAD∩平面ABCD＝AD，CD平面ABCD，

    CD⊥AD，∴CD⊥平面PAD.

    又CD平面PCD，∴平面PAD⊥平面PCD.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    空间中一条线段AB的三视图中，俯视图是长度为1的线段，侧视图是长度为2的线段，则线段AB的长度的取值范围是(　　)

    A．(0,2]                                                        B．[2，]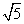

    C．[2,3]                                                        D．[2，]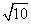

    查看答案和解析>>

    科目：高中数学 来源： 题型：


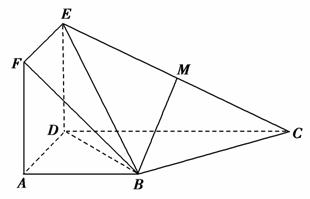
    如图，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，AB＝AD＝2，CD＝4，M为CE的中点．

    (1)求证：BM∥平面ADEF；

    (2)求证：平面BDE⊥平面BEC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设下图是某几何体的三视图，则该几何体的体积为(　　)

    A.π＋12                                                     B.π＋18

    C．9π＋42                                                    D．36π＋18

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如下的三个图中，上面是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出(单位：cm)．

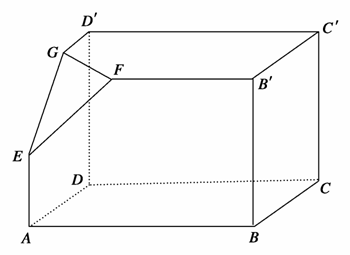
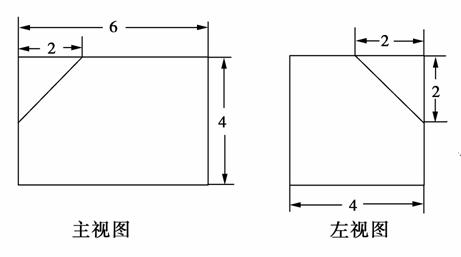
    (1)在主视图下面，按照画三视图的要求画出该多面体的俯视图；

    (2)按照给出的尺寸，求该多面体的体积

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知平面外一点P和平面内不共线三点A、B、C，A′、B′、C′分别在PA、PB、PC上，若延长A′B′、B′C′、A′C′与平面分别交于D、E、F三点，则D、E、F三点(　　)

    A．成钝角三角形　　　　　                          B．成锐角三角形

    C．成直角三角形                                          D．在一条直线上

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在棱长为2的正方体ABCD－A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1，AD的中点，那么异面直线OE与FD1所成角的余弦值等于(　　)

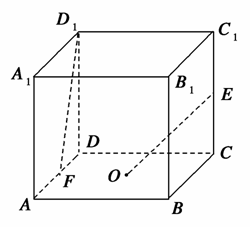
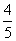    A.　　　B.　　　C.　　　D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设l为直线，α，β是两个不同的平面．下列命题中正确的是(　　)

    A．若l∥α，l∥β，则α∥β

    B．若l⊥α，l⊥β，则α∥β

    C．若b⊥α，l∥β，则α∥β

    D．若α⊥β，l∥α，则l⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为(　　)

    A.π                                                         B．4π

    C．4π                                                     D．6π

    查看答案和解析>>

    同步练习册答案