
分析 (1)令2x=t,得出关于t的函数g(t)=2t2-2t-1,根据二次函数的性质得出g(t)的值域即可f(x)的值域;
(2)分离参数a可得a=$\frac{1}{2}$($\frac{1}{{2}^{x}}$+$\frac{1}{2}$)2-$\frac{1}{8}$,再用换元法得出右侧函数的值域,从而得出a的范围.
解答 解:(1)当a=1时,f(x)=2•4x-2x-1=2(2x)2-2x-1,
令t=2x,由x∈[-4,0],得t∈[$\frac{1}{16}$,1].
设g(t)=2t2-t-1=2(t-$\frac{1}{4}$)2-$\frac{9}{8}$,t∈[$\frac{1}{16}$,1],
∴y=g(t)在$[\frac{1}{16},\frac{1}{4}]$单调递减,在$[\frac{1}{4},1]$单调递增,
∴当t=$\frac{1}{4}$时,g(t)取得最小值g($\frac{1}{4}$)=-$\frac{9}{8}$,
当t=1时,g(t)取得最大值g(1)=0,
∴f(x)在[-4,0]上的值域为[-$\frac{9}{8}$,0].
(2)法一:关于x的方程2a(2x)2-2x-1=0有实数解,设2x=m>0,
等价于方程2am2-m-1=0在m∈(0,+∞)上有解.
记g(m)=2am2-m-1,
当a=0时,解为m=-1<0,不成立.
当a<0时,开口向下,对称轴m=$\frac{1}{4a}$<0,
过点(0,-1),不成立.
当a>0时,开口向上,对称轴m=$\frac{1}{4a}$>0,
过点(0,-1),必有一个根为正,所以a>0.
∴实数a的取值范围为a>0.
法二:关于x的方程2a(2x)2-2x-1=0有实数解,
∴a=$\frac{{2}^{x}+1}{2•{4}^{x}}$=$\frac{1}{2}$($\frac{1}{{2}^{x}}$+$\frac{1}{{4}^{x}}$)=$\frac{1}{2}$($\frac{1}{{2}^{x}}$+$\frac{1}{2}$)2-$\frac{1}{8}$,
令$t=\frac{1}{2^x}$,t>0,则$a=\frac{1}{2}(t+{t^2})=\frac{1}{2}{(t+\frac{1}{2})^2}-\frac{1}{8}$在(0,+∞)单调递增,
∴实数a的取值范围为a>0.
点评 本题考查了换元法与函数值域的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
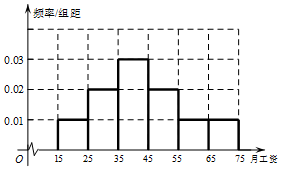 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:| 月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
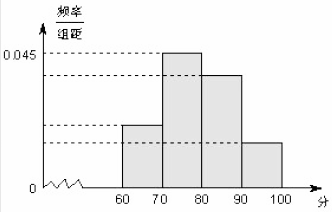
| 分数段 | 频数 | |
| [60,70) | p | |
| [70,80) | 90 | |
| [80,90) | 60 | |
| [90,100] | 20 | q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com