
分析 利用新定义,特殊角的三角函数值,求得要求式子的值.
解答 解:∵运算a⊕b=a2+2ab-b2,则cos$\frac{π}{6}$⊕sin$\frac{π}{6}$=${cos}^{2}\frac{π}{6}$+2cos$\frac{π}{6}$sin$\frac{π}{6}$-${sin}^{2}\frac{π}{6}$=$\frac{3}{4}$+2•$\frac{\sqrt{3}}{2}•\frac{1}{2}$-$\frac{1}{4}$=$\frac{1+\sqrt{3}}{2}$,
故答案为:$\frac{{1+\sqrt{3}}}{2}$.
点评 本题主要考查新定义,特殊角的三角函数值,属于基础题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:选择题
 如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )
如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )| A. | $\frac{π}{2}-\frac{{\sqrt{3}}}{8}$ | B. | $\frac{π}{2}-\frac{{3\sqrt{3}}}{8}$ | C. | $\frac{3π}{2}-\frac{{\sqrt{3}}}{8}$ | D. | $\frac{3π}{2}-\frac{{3\sqrt{3}}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | x2-y2=1 | D. | x2-$\frac{{y}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b都能被5整除 | B. | a,b都不能被5整除 | ||
| C. | a,b有一个能被5整除 | D. | a,b有一个不能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
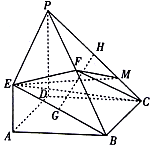 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | [-1,0] | C. | (-∞,-1)∪(0,+∞) | D. | (-∞,-1]∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ζ | 0 | 1 | 2 | 3 |
| P | 0.7 | 0.1 | 0.1 | 0.1 |
| η | 0 | 1 | 2 | 3 |
| p | 0.5 | 0.3 | 0.2 | 0 |
| A. | 甲比乙质量好 | B. | 乙比甲质量好 | C. | 甲与乙质量相同 | D. | 无法判定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com