
分析 (1)依题意,可得0°<90°-B<A<90°,sinA>sin(90°-B)=cosB,同理可得sinB>cosA,于是,可知点P位于第四象限,从而可化简所求关系式,得到答案.
(2)利用同角三角函数的基本关系式,结合已知条件求出sinx,cosx,即可求出求tanx的值.
解答 解:(1)解:因为△ABC为锐角三角形,
所以0°<A,B,C<90°,所以0°<90°-B<A<90°,
所以sinA>sin(90°-B)=cosB,
同理,sinB>cosA,即点P位于第二象限.
所以$\frac{|cosα|}{sin(\frac{3}{2}π+α)}$+$\frac{sin(π-α)}{|sinα|}$+$\frac{|tanα|}{tanα}$
=$\frac{-cosα}{-cosα}$+$\frac{sinα}{sinα}$+$\frac{-tanα}{tanα}$
=1;
(2)∵x∈($\frac{π}{4},\frac{π}{2}$),
∴sinx-cosx>0,sinx+cosx>0,
于是$\left\{\begin{array}{l}{sinx-cosx=\sqrt{1-2sinxcosx}}\\{sinx+cosx=\sqrt{1+2sinxcosx}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{sinx=\frac{24}{25}}\\{cosx=\frac{7}{25}}\end{array}\right.$,
所以tanx=$\frac{sinx}{cosx}$=$\frac{24}{7}$.
点评 本题考查同角三角函数的基本关系式的应用,三角函数的化简求值,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2016}{{2}^{2016}}$ | B. | 2016×22015 | C. | 2016×22016 | D. | $\frac{2016}{{2}^{2015}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
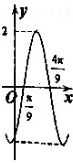
| A. | 函数f(x)的最小正周期为$\frac{π}{2}$ | B. | $φ=\frac{π}{9}$ | ||
| C. | 函数f(x)在区间$[0,\frac{π}{4}]$上是增函数 | D. | 函数f(x)的图象关于直线$x=\frac{5π}{6}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2=1 | B. | x2-y+3=0 | C. | $y=\sqrt{x-3}+\sqrt{2-x}+3$ | D. | 以上都不是 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 48种 | C. | 64种 | D. | 72种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{2}{5}$ | C. | -$\frac{2}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 0或-2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com