
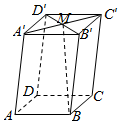
| A. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
分析 由空间向量加法法则得到$\overrightarrow{BM}$=$\overrightarrow{B{B}^{'}}$+$\overrightarrow{{B}^{'}M}$=$\overrightarrow{A{A}^{'}}$+$\frac{1}{2}$$\overrightarrow{BD}$=$\overrightarrow{A{A}^{'}}$+$\frac{1}{2}$($\overrightarrow{BA}+\overrightarrow{AD}$),由此能求出结果.
解答  解:∵在平行六面体ABCD-A′B′C′D′中,
解:∵在平行六面体ABCD-A′B′C′D′中,
$\overrightarrow{AB}=\vec a$,$\overrightarrow{AD}=\overrightarrow b$,$\overrightarrow{AA'}=\overrightarrow c$,
∴$\overrightarrow{BM}$=$\overrightarrow{B{B}^{'}}$+$\overrightarrow{{B}^{'}M}$=$\overrightarrow{A{A}^{'}}$+$\frac{1}{2}$$\overrightarrow{BD}$=$\overrightarrow{A{A}^{'}}$+$\frac{1}{2}$($\overrightarrow{BA}+\overrightarrow{AD}$)
=$\overrightarrow{c}$+$\frac{1}{2}$(-$\overrightarrow{a}$+$\overrightarrow{b}$)=-$\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}+\overrightarrow{c}$.
故选:A.
点评 本题考查空间向量的求法,是基础题,解题时要认真审题,注意空间向量坐标运算法则的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b⊥a,则b∥α | B. | 若a∥α,a∥β,则α∥β | C. | 若α⊥β,a⊥α,则a∥β | D. | 若α⊥γ,β∥γ,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y=0 | B. | 2x-y+5=0 | C. | 2x+y+3=0 | D. | x-2y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
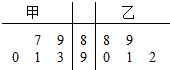 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {-1,0,2} | C. | {-1,0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com