
���� ��1�����f��x���ĵ�����ͨ������k����ż�ԣ���������ĵ������伴�ɣ�
��2������ת��Ϊa��$\frac{{x}^{2}}{2x+2lnx}$�������x��[e��+�ޣ����������h��x��=$\frac{{x}^{2}}{2x+2lnx}$�����h��x���ĵ������Ӷ����h��x������Сֵ�����a�ķ�Χ���ɣ�
��3�����g��x���ı���ʽ�����x2��ֵ���õ�g��x2��-x2+1=-2ln��1+$\sqrt{1-m}$��+$\sqrt{1-m}$����$\sqrt{1-m}$=t����t��0����h��t��=-2ln��1+t��+t�����h��t�������ֵ�Ǹ������Ӷ��Ƚϴ�С��
��� �⣺��1��f��x��=x2-2a��-1��klnx��k��N*��a��R��a��0���Ķ������ǣ�0��+�ޣ���
��f�䣨x��=$\frac{{2x}^{2}-2{a��-1��}^{k}}{x}$��
kΪ����ʱ��f�䣨x��=$\frac{{2x}^{2}+2a}{x}$��0��f��x���ڣ�0��+�ޣ�������
kΪż��ʱ��f�䣨x��=$\frac{{2x}^{2}-2a}{x}$��
��f�䣨x����0����ã�x��$\sqrt{a}$����f�䣨x����0����ã�0��x��$\sqrt{a}$��
��f��x���ڣ�0��$\sqrt{a}$���ݼ����ڣ�$\sqrt{a}$��+�ޣ�������
��2��k=2006ʱ��f��x��=x2-2alnx������x�IJ���ʽf��x����2ax�������x��[e��+�ޣ��������
��x2-2alnx��2ax�������x��[e��+�ޣ��������
��a��$\frac{{x}^{2}}{2x+2lnx}$�������x��[e��+�ޣ��������
��h��x��=$\frac{{x}^{2}}{2x+2lnx}$����h�䣨x��=$\frac{2x��x-1+2lnx��}{{��2x+2lnx��}^{2}}$��0��
h��x����[e��+�ޣ�������h��x����Сֵ=h��e��=$\frac{{e}^{2}}{2e+2}$��
��0��a��$\frac{{e}^{2}}{2e+2}$��
��3��k=2016ʱ��f��x��=x2-2alnx��
g��x��=$\frac{1}{a}$f��x��-$\frac{1}{a}$x2+x-$\frac{m}{x}$=-2lnx+x-$\frac{m}{x}$����x��0����
g�䣨x��=-$\frac{2}{x}$+1+$\frac{m}{{x}^{2}}$=$\frac{{x}^{2}-2x+m}{{x}^{2}}$��
����g��x����2����ֵ�㣬��g�䣨x��=0��2������ȵ�ʵ������
�ⷽ��x2-2x+m=0����ã�x2=1+$\sqrt{1-m}$��m��1����
��g��x2��-x2+1=-2ln��1+$\sqrt{1-m}$��+1-$\frac{m}{1+\sqrt{1-m}}$=-2ln��1+$\sqrt{1-m}$��+$\sqrt{1-m}$��
��$\sqrt{1-m}$=t����t��0��
��h��t��=-2ln��1+t��+t����h�䣨t��=$\frac{1-t}{1+t}$��h�壨t��=-$\frac{2}{{��1+t��}^{2}}$��0��
��h�䣨t���ڣ�0��+�ޣ��ݼ���h�䣨t��max=h�䣨0��=1��h�䣨1��=0��
��x�ʣ�0��1��ʱ��h�䣨t����0��x�ʣ�1��+�ޣ�ʱ��h�䣨t����0��
��h��t���ڣ�0��1���������ڣ�1��+�ޣ��ݼ���
��h��t��max=h��1��=-2ln2+1��0��
��h��t����0�ڣ�0��+�ޣ��������
��g��x2����x2-1��
���� ���⿼���������ĵ����ԡ���ֵ���⣬���鵼����Ӧ�ã�������������⣬����ת��˼�룬������һ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | ��2��1�� | C�� | ��0��1+$\frac{1}{a}$�� | D�� | ��2��1+a�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
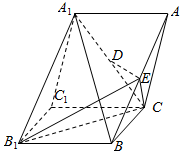 ��ͼ����������A1B1C1-ABC����D��E�ֱ���A1C��AB���е㣮
��ͼ����������A1B1C1-ABC����D��E�ֱ���A1C��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
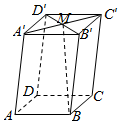
| A�� | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | B�� | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C�� | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D�� | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=0 | B�� | $x=\frac{��}{4}$ | C�� | $x=\frac{��}{2}$ | D�� | x=�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com