练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在锐角△ABC中，角A、B、C的对边分别为a、b、c，且满足(2a－c)cos B＝

    bcos C.

    (1)求角B的大小；

    (2)设m＝(sin A,1)，n＝(3，cos 2A)，试求m·n的取值范围．


    解　(1)因为(2a－c)cos B＝bcos C，

    所以(2sin A－sin C)cos B＝sin Bcos C，

    即2sin Acos B＝sin Ccos B＋sin Bcos C

    ＝sin(C＋B)＝sin A.

    而sin A>0，所以cos B＝.

    又∵0°<B<180°，∴B＝60°.

    (2)因为m＝(sin A,1)，n＝(3，cos 2A)，

    所以m·n＝3sin A＋cos 2A＝3sin A＋1－2sin2A

    由所以30°<A<90°，从而sin A∈，

    故m·n的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知向量，，，则执行如图所示的程序框图，输出的值(    )

    A.           B.           C.           D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    “是“直线与圆相交”的

    A．充分不必要条件   B. 必要不充分条件   C．充要条件  D. 既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知＝(1,2)，＝(4,1)，＝(0，－1)，则△ABC的形状是______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


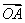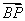    已知△ABO三顶点的坐标为A(1,0)，B(0,2)，O(0,0)，P(x，y)是坐标平面内一点，且满足·≤0，·≥0，则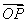·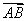的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若e1、e2是夹角为的单位向量，且向量a＝2e1＋e2，向量b＝－3e1＋2e2，则a·b＝______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不共线向量a，b的夹角为小于120°的角，且|a|＝1，|b|＝2，已知向量c＝a＋2b，求|c|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     给出下列命题：

    ①两个具有公共终点的向量，一定是共线向量；

    ②两个向量不能比较大小，但它们的模能比较大小；

    ③λa＝0 (λ为实数)，则λ必为零；

    ④λ，μ为实数，若λa＝μb，则a与b共线．

    其中错误命题的序号为____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若sin α＝，＝________.

    查看答案和解析>>

    同步练习册答案