
| A. | 0或$4-2\sqrt{3}$ | B. | $4+2\sqrt{3}$ | C. | 0 | D. | $4±2\sqrt{3}$ |
分析 作出y=f(x)与y=kx的图象,令两图象有两个交点得出k的值.
解答 解:∵g(x)=f(x)-kx有两个零点,
∴y=f(x)与y=kx的图象有两个交点,
作出f(x)与y=kx的图象如图所示: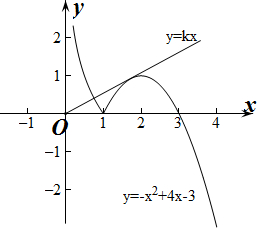
由图象可知当k=0或当直线y=kx与y=-x2+4x-3相切时,两图象有2个交点.
把y=kx代入y=-x2+4x-3得x2+(k-4)x+3=0,
令△=(k-4)2-12=0得k=4±2$\sqrt{3}$,
当k=4+2$\sqrt{3}$时,切点横坐标x=-$\sqrt{3}$,不符合题意;
∴k=4-2$\sqrt{3}$.
∴当k=0或k=4-2$\sqrt{3}$时,两图象有两个交点.
故选A.
点评 本题考查了函数零点与函数图象的关系,属于中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
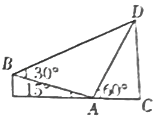 如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.
如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3.5 | 4.5 | 5.5 | 6.5 |
| y | 3 | 4m | 4 | 5 |
| A. | 1 | B. | 0.85 | C. | 0.95 | D. | 0.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,4} | B. | {3,6} | C. | {1,3} | D. | {1,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com