
【题目】已知抛物线C: ![]() 的焦点为F,直线
的焦点为F,直线![]() 与y轴的交点为P,与C的交点为Q,且
与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求C的方程;
(2)过F的直线![]() 与C相交于A,B两点,若AB的垂直平分线
与C相交于A,B两点,若AB的垂直平分线![]() 与C相较于M,N两点,且A,M,B,N四点在同一圆上,求
与C相较于M,N两点,且A,M,B,N四点在同一圆上,求![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【解析】试题分析:(1)由已知条件,先求![]() 点的坐标,再由
点的坐标,再由![]() 及抛物线的焦半径公式列方程可求得
及抛物线的焦半径公式列方程可求得![]() 的值,从而可得抛物线C的方程;(2)由已知条件可知直线
的值,从而可得抛物线C的方程;(2)由已知条件可知直线![]() 与坐标轴不垂直,故可设直线
与坐标轴不垂直,故可设直线![]() 的点参式方程:
的点参式方程: ![]() ,代入
,代入![]() 消元得
消元得![]() .设
.设![]() 由韦达定理及弦长公式表示
由韦达定理及弦长公式表示![]() 的中点
的中点![]() 的坐标及
的坐标及![]() 长,同理可得
长,同理可得![]() 的中点
的中点![]() 的坐标及
的坐标及![]() 的长.由于
的长.由于![]() 垂直平分线
垂直平分线![]() ,故
,故![]() 四点在同一圆上等价于
四点在同一圆上等价于![]() ,由此列方程可求得
,由此列方程可求得![]() 的值,进而可得直线
的值,进而可得直线![]() 的方程.
的方程.
试题解析:(1)设![]() ,代入
,代入![]() ,得
,得![]() .由题设得
.由题设得![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() ,∴C的方程为
,∴C的方程为![]() ;(2)由题设知
;(2)由题设知![]() 与坐标轴不垂直,故可设
与坐标轴不垂直,故可设![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() .设
.设![]() 则
则![]()
![]() .故
.故![]() 的中点为
的中点为![]() .又
.又![]() 的斜率为
的斜率为![]() 的方程为
的方程为![]() .将上式代入
.将上式代入![]() ,并整理得
,并整理得![]() .设
.设![]() 则
则![]() .故
.故![]() 的中点为
的中点为 .
.
由于![]() 垂直平分线
垂直平分线![]() ,故
,故![]() 四点在同一圆上等价于
四点在同一圆上等价于![]() ,从而
,从而![]() 即
即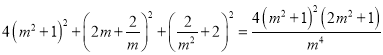 ,化简得
,化简得![]() ,解得
,解得![]() 或
或![]() .所求直线
.所求直线![]() 的方程为
的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次测验共有4个选择题和2个填空题,每答对一个选择题得20分,每答对一个填空题得10分,答错或不答得0分,若某同学答对每个选择题的概率均为 ![]() ,答对每个填空题的概率均为
,答对每个填空题的概率均为 ![]() ,且每个题答对与否互不影响.
,且每个题答对与否互不影响.
(1)求该同学得80分的概率;
(2)若该同学已经答对了3个选择题和1个填空题,记他这次测验的得分为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间四边形ABCD的两条对角线的长AC=6,BD=8,AC与BD所成的角为30o , E,F,G,H分别是AB,BC,CD,DA的中点,求四边形EFGH的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCED中,PD⊥面ABCD,四边形ABCD为平行四边形,∠DAB=60°,AB=PA=2AD=4, 
(1)若E为PC中点,求证:PA∥平面BDE
(2)求三棱锥D﹣BCP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有老年人30人,中年人90人,青年人60人,为了调查他们的身体健康状况,采用分层抽样的方法从他们中间抽取一个容量为36的样本,则应抽取老年人的人数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,
, ![]() 为椭圆的半焦距,且
为椭圆的半焦距,且![]() ,过点
,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别交于另两点
分别交于另两点![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的面积;
的面积;
(3)若线段![]() 的中点在
的中点在![]() 轴上,求直线
轴上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
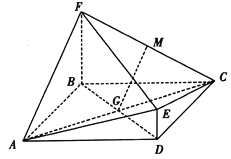
【题目】如图,菱![]() 与四边形BDEF相交于BD,
与四边形BDEF相交于BD, ![]() 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点, ![]() .
.
(I)求证:GM//平面CDE;
(II)求证:平面ACE⊥平面ACF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以O为极点,
为参数),以O为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆![]() 的普通方程;
的普通方程;
(Ⅱ)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆C的交点为
与圆C的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com