
已知椭圆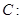
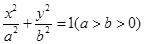 的离心率为
的离心率为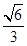 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为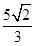 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知动直线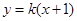 与椭圆
与椭圆 相交于
相交于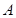 、
、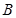 两点. ①若线段
两点. ①若线段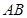 中点的横坐标为
中点的横坐标为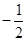 ,求斜率
,求斜率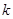 的值;②若点
的值;②若点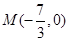 ,求证:
,求证: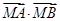 为定值.
为定值.
(Ⅰ)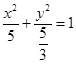 ;(Ⅱ)①
;(Ⅱ)① ;②
;② .
.
解析试题分析:(Ⅰ)根据已知条件可设椭圆方程为: ,则有
,则有 ,
,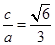 ,
, ,求解即可得到
,求解即可得到 和
和 的值,将对应的解代入椭圆方程即可;(Ⅱ)①将直线方程
的值,将对应的解代入椭圆方程即可;(Ⅱ)①将直线方程 代入椭圆方程求得,
代入椭圆方程求得, ,求得
,求得 、
、 两点的横坐标之和为
两点的横坐标之和为 ,由已知条件“
,由已知条件“ 中点的横坐标为
中点的横坐标为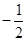 ”,得到
”,得到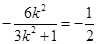 ,从而解得
,从而解得 的值;
的值;
②根据①的 、
、 两点的坐标求得
两点的坐标求得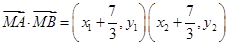 ③,结合
③,结合 、
、 两点坐标满足直线方程
两点坐标满足直线方程 ,将③式化简整理得
,将③式化简整理得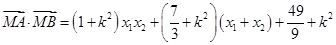 ,再由①中的根与系数的关系:
,再由①中的根与系数的关系: ,
,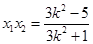 ,代入化简即可.
,代入化简即可.
试题解析:(Ⅰ)因为 满足
满足 ,
,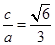 ,
, ,
,
解得 ,
, ,
,
则椭圆方程为: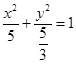 . 3分
. 3分
(Ⅱ)①将 代入
代入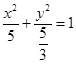 中得,
中得, ,
,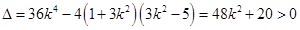 ,
,
设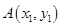 ,
, ,则
,则 ,
,
因为 中点的横坐标为
中点的横坐标为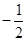 ,所以
,所以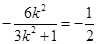 ,
,
解得 . 6分
. 6分
②由①知, ,
,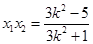 ,
,
所以

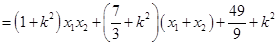
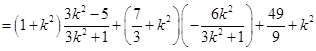
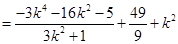
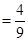 . 12分
. 12分
考点:1.椭圆的标准方程;2.椭圆的性质;3.方程的根与系数的关系;4.中点坐标公式;5.平面向量的数量积


科目:高中数学 来源: 题型:解答题
如图,已知椭圆 的方程为
的方程为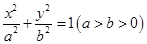 ,双曲线
,双曲线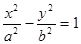 的两条渐近线为
的两条渐近线为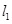 、
、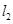 .过椭圆
.过椭圆 的右焦点
的右焦点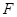 作直线
作直线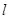 ,使
,使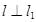 ,又
,又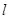 与
与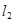 交于点
交于点 ,设
,设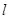 与椭圆
与椭圆 的两个交点由上至下依次为
的两个交点由上至下依次为 、
、 .
.
(1)若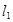 与
与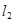 的夹角为
的夹角为 ,且双曲线的焦距为
,且双曲线的焦距为 ,求椭圆
,求椭圆 的方程;
的方程;
(2)求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系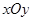 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为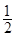 的椭圆E的一个焦点为圆
的椭圆E的一个焦点为圆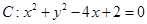 的圆心.
的圆心.
⑴求椭圆E的方程;
⑵设P是椭圆E上一点,过P作两条斜率之积为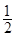 的直线
的直线 ,当直线
,当直线 都与圆
都与圆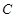 相切时,求P点坐标.
相切时,求P点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知中心在原点O,焦点在x轴上,离心率为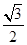 的椭圆过点
的椭圆过点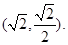
(1)求椭圆的方程;
(2)设不过原点O的直线 与该椭圆交于P,Q两点,满足直线
与该椭圆交于P,Q两点,满足直线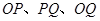 的斜率依次成等比数列,
的斜率依次成等比数列,
求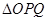 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知中心在原点的双曲线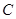 的一个焦点是
的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 。
。
(1)求双曲线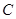 的方程;
的方程;
(2)若以 为斜率的直线
为斜率的直线 与双曲线
与双曲线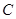 相交于两个不同的点
相交于两个不同的点 ,且线段
,且线段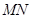 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为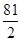 ,求
,求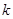 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com