
分析 (1)根据f(x)的解析式,求出a的值,从而求出g(x)的解析式,判断函数的奇偶性即可;
(2)根据函数单调性的定义证明即可;
(3)根据1+ax∈(1,+∞),从而得到$\frac{2}{{1+{a^x}}}∈(0,2)$,求出g(x)的值域即可.
解答 解:(1)∵f(x)=3x,
∴f(a+2)=3a+2=81,解得a=2.
∵$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}$(x∈R),
∴$g(-x)=\frac{{1-{2^{-x}}}}{{1+{2^{-x}}}}=\frac{{{2^x}-1}}{{{2^x}+1}}=-g(x)$,
即函数g(x)是奇函数.
证明:(2)任取x1,x2∈R,且x1<x2,
则$g({x_1})-g({x_2})=\frac{{1-{a^{x_1}}}}{{1+{a^{x_2}}}}-\frac{{1-{a^{x_2}}}}{{1+{a^{x_2}}}}$
=$\frac{{(1-{a^{x_1}})(1+{a^{x_2}})-(1-{a^{x_2}})(1+{a^{x_1}})}}{{(1+{a^{x_1}})(1+{a^{x_2}})}}=\frac{{2({a^{x_2}}-{a^{x_1}})}}{{(1+{a^{x_1}})(1+{a^{x_2}})}}$.
∵x1<x2,a>1,
∴${a^{x_2}}-{a^{x_1}}>0$,$(1+{a^{x_1}})(1+{a^{x_2}})>0$,
∴g(x1)-g(x2)>0,
即g(x1)>g(x2),
故函数g(x)在R上单调递减.
解:(3)∵$g(x)=\frac{{1-{a^x}}}{{1+{a^x}}}=\frac{2}{{1+{a^x}}}-1$,x∈R,
∴1+ax∈(1,+∞),
从而$\frac{2}{{1+{a^x}}}∈(0,2)$,
∴g(x)∈(-1,1)
故函数g(x)的值域为(-1,1)
点评 本题考查了函数的奇偶性问题,考查定义判断函数的单调性,考查求函数的值域问题,是一道中档题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1000件 | B. | 1200件 | C. | 1400件 | D. | 1600件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
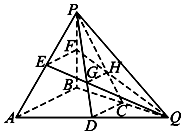 如图所示,在三棱锥PABQ中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH.求证:
如图所示,在三棱锥PABQ中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M⊆N | B. | M?N | C. | M=N | D. | M∩N=Φ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
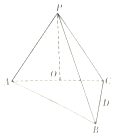 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com