
分析 (1)求出f(x)的定义域确定出A,表示出B中不等式的解集,根据A为B的子集,确定出a的范围即可;
(2)由A与B的交集为空集,确定出a的范围即可.
解答 解:(1)由函数f(x)=$\sqrt{4-x}$+lg(3x-9),得到$\left\{\begin{array}{l}{4-x≥0}\\{{3}^{x}-9>0}\end{array}\right.$,
解得:2<x≤4,即A=(2,4],
由题意得:B=(a,a+3),
∵A⊆B,
∴a的范围1<a≤2;
(2)∵A∩B=∅,
∴a+3≤2或a≥4,
解得:a≤-1或a≥4.
点评 此题考查了交集及其运算,以及集合的包含关系判断及应用,熟练掌握交集的定义是解本题的关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
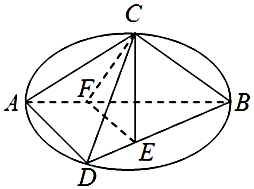 如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.
如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com