
分析 (1)由三角函数恒等变换化简解析式可得f(x)=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)+$\frac{1}{2}$,由正弦函数的图象和性质即可求得最小正周期,最小值.
(2)由2kπ$-\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,即可解得f(x)的单调增区间.
(3)由(1)的解析式列出表格,在平面坐标系中描出五个点,然后用平滑的曲线作出函数的图象即可.
解答 解:(1)∵f(x)=sin2x+sinxcosx
=$\frac{1-cos2x}{2}$+$\frac{1}{2}$sin2x
=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)+$\frac{1}{2}$.
∴最小正周期T=$\frac{2π}{2}$=π,最小值为$\frac{1}{2}-$$\frac{\sqrt{2}}{2}$.
(2)∵由2kπ$-\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,解得:kπ$-\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$,k∈Z,
∴f(x)的单调增区间为:[kπ$-\frac{π}{8}$,kπ+$\frac{3π}{8}$],k∈Z.
(3)列表如下:
| 2x-$\frac{π}{4}$ | -$\frac{5π}{4}$ | -$\frac{3π}{4}$ | -$\frac{π}{4}$ | $\frac{π}{4}$ | $\frac{3π}{4}$ |
| x | -$\frac{π}{2}$ | -$\frac{π}{4}$ | 0 | $\frac{π}{4}$ | $\frac{π}{2}$ |
| y | 1 | 0 | 0 | 1 | 1 |
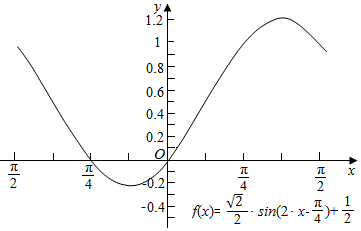
点评 本题主要考查了三角函数恒等变换的应用,考查了正弦函数的图象和性质,五点法作函数y=Asin(ωx+φ)的图象,要求熟练掌握五点作图法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题 | B. | ¬q是假命题 | C. | p∧(¬q)是真命题 | D. | (¬p)∨q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
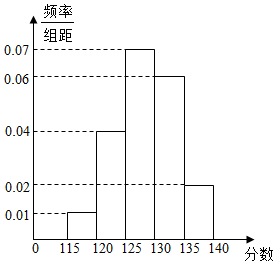 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $-\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $-\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com