练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    对函数f(x)＝3x2＋ax＋b作代换x＝g(t)，则总不改变f(x)值域的代换是(　　)

    A．g(t)＝log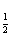t                                              B．g(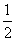t)＝()t

    C．g(t)＝(t－1)2                                            D．g(t)＝cost


    　A

    [解析]　只有A中函数的值域与f(x)中x的取值范围一致，即R，所以只有A中函数代换后f(x)值域不变．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知a>b，函数f(x)＝(x－a)·(x－b)的图像如图所示，则函数g(x)＝loga(x＋b)的图像可能为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝x3－3x＋a有3个不同的零点，则实数a的取值范围是(　　)

    A．(－2,2)                                                    B．[－2,2]

    C．(－∞，－1)                                             D．(1，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等边三角形的边长为x，面积为y，则y与x之间的函数关系式为(　　)

    A．y＝x2                                                       B．y＝x2

    C．y＝x2                                                D．y＝x2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某公司欲投资13亿元进行项目开发，现有以下6个项目可供选择.

    项目

    A

    B

    C

    D

    E

    F

    投资额(亿元)

    5

    2

    6

    4

    6

    1

    利润(亿元)

    0.55

    0.4

    0.6

    0.5

    0.9

    0.1

    设计一个投资方案，使投资13亿元所获利润大于1.6亿元，则应选的项目是________(只需写出项目的代号)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若幂函数y=f(x)的图象过点(2,),则函数f(x)的解析式为f(x)=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     给出以下命题:

    ①函数f(x)=|log2x2|既无最大值也无最小值;

    ②函数f(x)=|x2-2x-3|的图象关于直线x=1对称;

    ③若函数f(x)的定义域为(0,1),则函数f(x2)的定义域为(-1,1);

    ④若函数f(x)满足|f(-x)|=|f(x)|,则函数f(x)或是奇函数或是偶函数;

    ⑤设定义在R上的函数f(x)满足:对任意x1,x2∈R,x1<x2,有f(x1)-f(x2)<x1-x2恒成立,则函数F(x)=f(x)-x在R上是单调增函数.

    其中正确的命题是　　　　(填序号) 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若sinθ·cosθ＝，则tanθ＋的值是(　　)

    A．－2                                                          B．2

    C．±2                                                           D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知ω是正实数，且函数f(x)＝2sinωx在[－，]上是增函数，那么(　　)

    A．0<ω≤                                                 B．0<ω≤2

    C．0<ω≤                                               D．ω≥2

    查看答案和解析>>

    同步练习册答案