
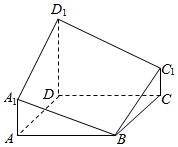
 如图所示的多面体是经过正四棱柱底面顶点B作截面A1BC1D1后形成的.已知AB=1,A1A=C1C=$\frac{1}{2}{D_1}$D,D1B与底面ABCD所成的角为$\frac{π}{3}$,则这个多面体的体积为$\frac{\sqrt{6}}{2}$.
如图所示的多面体是经过正四棱柱底面顶点B作截面A1BC1D1后形成的.已知AB=1,A1A=C1C=$\frac{1}{2}{D_1}$D,D1B与底面ABCD所成的角为$\frac{π}{3}$,则这个多面体的体积为$\frac{\sqrt{6}}{2}$. 分析 由题意画出图形,连接BD,BD1,可得∠${D}_{1}BD=\frac{π}{3}$,在底面正方形中,由AB=1,求得BD=$\sqrt{2}$,在Rt△D1DB中,解直角三角形求得DD1,求出直角梯形ADD1A1的面积,然后由棱锥的体积公式求得答案.
解答 解:如图,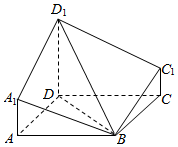
连接BD,BD1,则∠${D}_{1}BD=\frac{π}{3}$,
在底面正方形中,由AB=1,得BD=$\sqrt{2}$,
在Rt△D1DB中,由BD=$\sqrt{2}$,∠${D}_{1}BD=\frac{π}{3}$,
求得${D}_{1}D=BD•tan\frac{π}{3}=\sqrt{2}×\sqrt{3}=\sqrt{6}$,
∴A1A=C1C=$\frac{1}{2}{D_1}$D=$\frac{\sqrt{6}}{2}$,
则${S}_{AD{D}_{1}{A}_{1}}=\frac{1}{2}(\frac{\sqrt{6}}{2}+\sqrt{6})×1=\frac{3\sqrt{6}}{4}$,
∴多面体的体积为V=$2×\frac{1}{3}×\frac{3\sqrt{6}}{4}×1=\frac{\sqrt{6}}{2}$.
故答案为:$\frac{{\sqrt{6}}}{2}$.
点评 本题考查棱柱、棱锥及棱台体积的求法,考查空间想象能力和思维能力,是中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
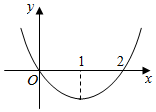
| A. | x=1是最小值点 | B. | x=0是极小值点 | ||
| C. | x=2是极小值点 | D. | 函数f(x)在(1,2)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [0,1] | C. | [0,1) | D. | [0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{15}}{6}$ | B. | -$\frac{\sqrt{15}}{6}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin$\frac{x}{2}$ | B. | y=cos2x | C. | y=sin(2x+$\frac{π}{4}$) | D. | y=tan(x-$\frac{π}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com