
分析 (Ⅰ)设等差数列{an}的公差为d,则d>0,运用等差数列的通项公式和求和公式,由等比数列的中项的性质,解方程可得d=2,即可得到所求通项公式;
(Ⅱ)求得bn=$2(\frac{1}{2n-1}-\frac{1}{2n+1})$,运用数列的求和方法:裂项相消求和,化简整理,即可得到所求和.
解答 解:(Ⅰ)设等差数列{an}的公差为d,因为a1=1,
∴a2+1=2+d,a4+1=2+3d,S4=4+6d,
∵a2+1,a4+1,S4成等比数列,
∴${({a_4}+1)^2}=({a_2}+1){S_4}$,
即(2+3d)2=(2+d)(4+6d),
解得d=2或$d=-\frac{2}{3}$.
∵等差数列{an}是递增数列,∴d=2,
∴an=2n-1;
(Ⅱ)∵${b_n}=\frac{a_n}{{{a_{n+1}}}}+\frac{{{a_{n+1}}}}{a_n}-2$
=$\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}-2$
=$(1-\frac{2}{2n+1})+(1+\frac{2}{2n-1})-2$=$2(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴${T_n}=2(1-\frac{1}{3})+2(\frac{1}{3}-\frac{1}{5})+…+2(\frac{1}{2n-1}-\frac{1}{2n+1}\;)$
=$2(1-\frac{1}{2n+1}\;)$=$\frac{4n}{2n+1}$.
点评 本题主要考查等差数列、等比数列的通项和求和公式的运用,数列求和方法:裂项相消求和等基础知识,考查运算求解能力,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
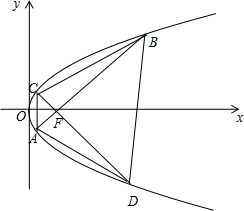 如图,在直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A,B,C,D四点.
如图,在直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A,B,C,D四点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的五面体中,四边形ABCD是矩形,平面ADF⊥平面ABEF,且AB∥EF,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,M是EF的中点,N在AM上.
在如图所示的五面体中,四边形ABCD是矩形,平面ADF⊥平面ABEF,且AB∥EF,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,M是EF的中点,N在AM上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
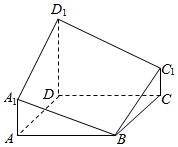 如图所示的多面体是经过正四棱柱底面顶点B作截面A1BC1D1后形成的.已知AB=1,A1A=C1C=$\frac{1}{2}{D_1}$D,D1B与底面ABCD所成的角为$\frac{π}{3}$,则这个多面体的体积为$\frac{\sqrt{6}}{2}$.
如图所示的多面体是经过正四棱柱底面顶点B作截面A1BC1D1后形成的.已知AB=1,A1A=C1C=$\frac{1}{2}{D_1}$D,D1B与底面ABCD所成的角为$\frac{π}{3}$,则这个多面体的体积为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com