已知函数f(x)=ax+lnx(a∈R).
(1)若a=2,求曲线y=f(x)在x=1处切线的斜率;
(2)当a<0时,求f(x)的单调区间;
(3)设g(x)=x2-2x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
解:(1)由已知

,…(2分)
∴f'(1)=2+1=3.
故曲线y=f(x)在x=1处切线的斜率为3.…(4分)
(2)求导函数可得

.…(5分)
当a<0时,由f'(x)=0,得
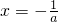
.
在区间
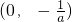
上,f'(x)>0;在区间
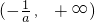
上,f'(x)<0,
所以,函数f(x)的单调递增区间为
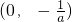
,单调递减区间为
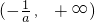
…(10分)
(3)由已知转化为f(x)
max<g(x)
max.
∵g(x)=x
2-2x+2=(x-1)
2+1,x
2∈[0,1],∴g(x)
max=2…(11分)
由(2)知,当a≥0时,f(x)在(0,+∞)上单调递增,值域为R,故不符合题意.
(或者举出反例:存在f(e
3)=ae
3+3>2,故不符合题意.)
当a<0时,f(x)在
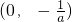
上单调递增,在
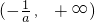
上单调递减,
故f(x)的极大值即为最大值,
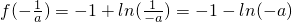
,
所以2>-1-ln(-a),所以ln(-a)>-3,
解得

.…(14分)
分析:(1)利用导数的几何意义,可求曲线y=f(x)在x=1处切线的斜率;
(2)求导函数,在区间
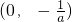
上,f'(x)>0;在区间
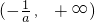
上,f'(x)<0,故可得函数的单调区间;
(3)由已知转化为f(x)
max<g(x)
max,可求g(x)
max=2,f(x)最大值-1-ln(-a),由此可建立不等式,从而可求a的取值范围.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查求参数的值,解题的关键是转化为f(x)
max<g(x)
max.

 ,…(2分)
,…(2分) .…(5分)
.…(5分)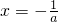 .
.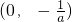 上,f'(x)>0;在区间
上,f'(x)>0;在区间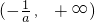 上,f'(x)<0,
上,f'(x)<0,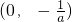 ,单调递减区间为
,单调递减区间为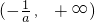 …(10分)
…(10分)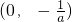 上单调递增,在
上单调递增,在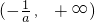 上单调递减,
上单调递减,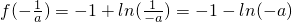 ,
, .…(14分)
.…(14分)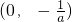 上,f'(x)>0;在区间
上,f'(x)>0;在区间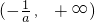 上,f'(x)<0,故可得函数的单调区间;
上,f'(x)<0,故可得函数的单调区间;

 阅读快车系列答案
阅读快车系列答案