
���� ��1��������ɵ�a��c�Ĺ�ϵ�������ɵ�a��b�Ĺ�ϵ�������Բ��a��b��c�Ĺ�ϵ���ɵ�a��b��ֵ�������õ���Բ���̣�
��2��������ɵ�M����Բ�ڣ����۹�M��ֱ��б�ʲ����ںʹ��ڣ�������Բ�ļ����귽�̣����A��B�����꣬���ù��ɶ����������ε������ʽ�����㼴�ɵõ���ֵ|OM|��
��� ��1���⣺������ɵ�2a��2c=2��$\sqrt{2}$��
����$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$����a2-b2=c2��
$\frac{5}{{a}^{2}}$+$\frac{3}{2{b}^{2}}$=1��
���a=2$\sqrt{2}$��b=2��
������Բ����Ϊ$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1��
��2��������ڶ���M��ʹ����M����ֱ��OM��ֱ��ֱ��l����ԲC
����������ͬ�Ľ���A��B��
����M��m��n��������M����Բ�ڣ�
��Ϊm2+2n2-8��0��
������$\overrightarrow{OA}$��$\overrightarrow{OB}$ʱ���ҹ�M��ֱ��б�ʲ�����ʱ��
����m2+2y2=8����y=m�����m=��$\frac{2\sqrt{6}}{3}$��
����|OM|=$\frac{2\sqrt{6}}{3}$��
����M��ֱ��б�ʴ���ʱ����OΪ���㣬x��Ϊ���ᣬ����������ϵ��
��x=��cos�ȣ�y=��sin�ȣ�������Բ���̿ɵæ�2=$\frac{8}{1+si{n}^{2}��}$��
��A����1���ȣ���B����2����+$\frac{��}{2}$����
���12=$\frac{8}{1+si{n}^{2}��}$����22=$\frac{8}{1+si{n}^{2}����+\frac{��}{2}��}$=$\frac{8}{1+co{s}^{2}��}$��
��ֱ�������εĹ��ɶ����ɵ�|AB|2=|OA|2+|OB|2
=$\frac{8}{1+si{n}^{2}��}$+$\frac{8}{1+co{s}^{2}��}$=$\frac{24}{��1+si{n}^{2}�ȣ���1+co{s}^{2}�ȣ�}$��
�������ε������ʽ�ɵ�
|OM|=$\frac{|OA|•|OB|}{|AB|}$��
����|OM|2=$\frac{|OA{|}^{2}•|OB{|}^{2}}{|AB{|}^{2}}$=$\frac{64}{24}$��
����|OM|Ϊ��ֵ$\frac{2\sqrt{6}}{3}$��
���Ͽɵã����������Ķ�������Բ�ڣ�|OM|Ϊ��ֵ$\frac{2\sqrt{6}}{3}$��
���� ���⿼����Բ�ķ��̺����ʣ���Ҫ������Բ�������ʹ�ʽ�ͷ��̵����ã�������Բ�ļ����귽�̵����ã�ͬʱ�������Ǻ����Ļ������ֵ�������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����֪F1��F2Ϊ˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$���������㣬��|F1F2|=2����������ԭ��OΪԲ�ģ�|F1F2|Ϊֱ����Բ���˫���ߵ���֧�ཻ��A��B���㣬�ҡ�F2ABΪ�������Σ���˫���ߵ�ʵ�᳤Ϊ$\sqrt{3}$-1��
��ͼ��ʾ����֪F1��F2Ϊ˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$���������㣬��|F1F2|=2����������ԭ��OΪԲ�ģ�|F1F2|Ϊֱ����Բ���˫���ߵ���֧�ཻ��A��B���㣬�ҡ�F2ABΪ�������Σ���˫���ߵ�ʵ�᳤Ϊ$\sqrt{3}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{2}$ | B�� | $\frac{2}{3}$ | C�� | 1 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
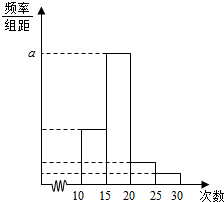 ��ijУ��һ�꼶ѧ���μӡ�����־Ը�ߡ����������ͳ�ƣ������ȡM��ѧ����Ϊ�������õ���M��ѧ���μӡ�����־Ը�ߡ���Ĵ������ݴ�����Ƶ����Ƶ��ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ���£�
��ijУ��һ�꼶ѧ���μӡ�����־Ը�ߡ����������ͳ�ƣ������ȡM��ѧ����Ϊ�������õ���M��ѧ���μӡ�����־Ը�ߡ���Ĵ������ݴ�����Ƶ����Ƶ��ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ���£�| ���� | Ƶ�� | Ƶ�� |
| [10��15�� | 5 | 0.25 |
| [15��20�� | 12 | n |
| [20��25�� | m | p |
| [25��30] | 1 | 0.05 |
| �ϼ� | M | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��-1�� | B�� | ��-3��5] | C�� | ��3��5] | D�� | ��-1��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com