
分析 理解仿射坐标的概念,利用空间向量的共线定理及数量积运算即可求解.
解答 解:①若$\overrightarrow{a}$=(2,0,-1)$\overrightarrow{o}$,$\overrightarrow{b}$=(1,0,2)$\overrightarrow{o}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=(2$\overrightarrow{i}$-$\overrightarrow{k}$)•($\overrightarrow{i}$+2$\overrightarrow{k}$)=2+3$\overrightarrow{i}$•$\overrightarrow{k}$-2=3cosθ,
∵0<θ<π,且$θ≠\frac{π}{2}$,∴$\overrightarrow{a}$•$\overrightarrow{b}$≠0;
②$\overrightarrow{a}=(x,y,0)_{\frac{π}{3}}$,$\overrightarrow{b}=(0,0,z)_{\frac{π}{3}}$,其中xyz≠0,向量$\overrightarrow{a}$的夹角取得最小值,两向量同向
存在实数λ>0,满足$\overrightarrow{a}$=λ$\overrightarrow{b}$,根据仿射坐标的定义,易知②为正确;
③已知$\overrightarrow{a}$=(x1,y1,z1)θ,$\overrightarrow{b}$=(x2,y2,z2)θ,则$\overrightarrow{a}$=(x1-x2)$\overrightarrow{i}$+(y1-y2)$\overrightarrow{j}$+(z1-z2)$\overrightarrow{k}$,
$\overrightarrow{a}-\overrightarrow{b}=({x}_{1}-{x}_{2},{y}_{1}-{y}_{2},{z}_{1}{-z}_{2})_{θ}$
④$\overrightarrow{OA}=(1,0,0)_{\frac{π}{3}}$,$\overrightarrow{OB}=(0,1,0)_{\frac{π}{3}}$,$\overrightarrow{OC}=(0,0,1)_{\frac{π}{3}}$已知,则三棱锥O-ABC为正四面体,棱长为1,∴表面积为S=4×$4×\frac{1}{2}×1×\frac{\sqrt{3}}{2}=\sqrt{3}$.
故答案为:②③.
点评 本题主要考察了向量的相关概念,综合性较强,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [-1,3] | C. | [3,5] | D. | [5,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高效 | 非高效 | 统计 | |
| 新课堂模式 | 60 | 30 | 90 |
| 传统课堂模式 | 40 | 50 | 90 |
| 统计 | 100 | 80 | 180 |
| P(K2≧K0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
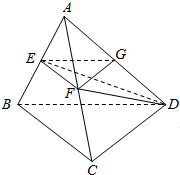 如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:
如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com