练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．执行如图所示的程序框图，如果输出的S值大于$\frac{5}{3}$，则输入的正整数N的最小值为（　　）
    A．4B．5C．6D．7

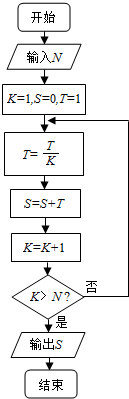
    分析 由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．

    解答 解：第一次执行完循环体后，T=1，S=1，K=2，不满足输出条件，
    再次执行完循环体后，T=$\frac{1}{2}$，S=$\frac{3}{2}$，K=3，不满足输出条件，
    再次执行完循环体后，T=$\frac{1}{6}$，S=$\frac{5}{3}$，K=4，不满足输出条件，
    再次执行完循环体后，T=$\frac{1}{24}$，S=$\frac{41}{24}$，K=5，满足输出条件，
    故输入的正整数N的值为4，
    故选：A．

    点评 本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

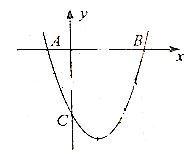    9．如图，已知二次函数y=ax2+bx-3的图象过坐标（-2，5），与x轴的两个交点分别为A，B（3，0）．与y轴的负半轴交于点C．
    （1）求二次函数的表达式；
    （2）在该函数图象上能否找到一点P，使∠POC=∠PCO？若能，请求出点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

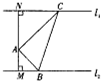    10．如图，A是两条平行直线之间的一定点，且点A到两条平行直线的距离分别为AM=1，AN=$\sqrt{3}$．设△ABC，AC⊥AB，且顶点B、C分别在两条平行直线上运动，则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若球的半径为a，球的最大截面面积为4π，则二项式（a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$）4的展开式中的常数项为24．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知a1=3，（2-an）•an+1=1，求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知定义在区间[a，a+2]上的奇函数y=f（x），当0＜x≤a+2时，f（x）=$\frac{1}{4}$（x-1）．若方程f（x）=x3+cx恰有三个不相等的实数根，则实数c的取值范围为$c=-\frac{1}{2}$或c＜-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知单位向量$\overrightarrow i，\overrightarrow j，\overrightarrow k$两两的夹角均为θ（0＜θ＜π，且θ≠$\frac{π}{2}$），若空间向量$\overrightarrow a$满足$\overrightarrow a=x\overrightarrow i+y\overrightarrow j+z\overrightarrow k（x，y，z∈R）$，则有序实数组（x，y，z）称为向量$\overrightarrow a$在“仿射”坐标系O-xyz（O为坐标原点）下的“仿射”坐标，记作$\overrightarrow a={（x，y，z）_θ}$有下列命题：
    ①已知$\overrightarrow a={（1，3，-2）_θ}，\overrightarrow b={（4，0，2）_θ}$，则$\overrightarrow a$•$\overrightarrow b$=0；
    ②已知$\overrightarrow a={（x，y，0）_{\frac{π}{3}}}，\overrightarrow b={（0，0，z）_{_{\frac{π}{3}}}}$其中xyz≠0，则当且仅当x=y时，向量$\overrightarrow a$，$\overrightarrow b$的夹角取得最小值；
    ③已知$\overrightarrow a={（{x_1}，{y_1}，{z_1}）_θ}，\overrightarrow b={（{x_2}，{y_2}，{z_2}）_θ}，则\overrightarrow a+\overrightarrow b={（{x_1}+{x_2}，{y_1}+{y_2}，{z_1}+{z_2}）_θ}$；
    ④已知$\overrightarrow{OA}={（1，0，0）_{\frac{π}{3}}}，\overrightarrow{OB}={（0，1，0）_{\frac{π}{3}}}，\overrightarrow{OC}={（0，0，1）_{\frac{π}{3}}}$，则三棱锥O-ABC的表面积S=$\sqrt{2}$，其中真命题有②③（写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．在等差数列{an}中，a9=$\frac{1}{2}$a12+6，则该数列的前11项和为132．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．从集合{1，2，3}中随机取一个元素，记为a，从集合{2，3，4}中随机取一个元素，记为b，则a≤b的概率为$\frac{8}{9}$．

    查看答案和解析>>

    同步练习册答案