

分析 根据三视图判断几何体的形状,根据它的几何性质得出AD⊥面BDC,DC=1,AD=1,BE⊥CD与E,DE=$\frac{1}{2}$,BE=$\frac{\sqrt{3}}{2}$,
利用三角形判断得出三角形BDC外接圆的半径r=1,构造长方体利用外接球的几何性质求解R即得出面积.
解答 解:根据三视图得出几何体为三棱锥,
AD⊥面BDC,DC=1,AD=1,BE⊥CD与E,DE=$\frac{1}{2}$,BE=$\frac{\sqrt{3}}{2}$,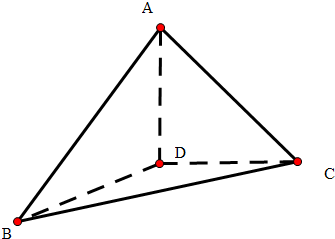
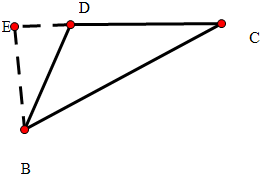
∴∠BDE=60°,BD=1,
∵在三角形BDC中,BD=DC=1,∠BDC=120°,
∴根据余弦定理得出:BC=$\sqrt{3}$,
∵利用正弦定理得出:$\frac{BC}{sin120°}$=2r
∴三角形BDC外接圆的半径r=1,直径为2,
∵三棱锥的外接球的半径R,d=AD=1,
利用球的几何性质得出:△BCD的外接圆的以DC为一边的内接矩形的边长$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
构造长方体棱长为:1,1,$\sqrt{3}$,可知长方体的外接球的直径2R=$\sqrt{{1}^{2}+{1}^{2}+3}$,
即R=$\frac{\sqrt{5}}{2}$,
∴它的外接球的表面积为4×π×( $\frac{\sqrt{5}}{2}$ )2=5π
故答案为:5π.
点评 本题考查了空间几何体的外接球的问题,充分利用几何性质,把立体问题转化为平面问题求解,考查了三角的定理的运用综合性较强,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,] | C. | [-1,1) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥γ,β⊥γ,则α∥β | B. | 若a⊥c,b⊥c,则a∥b | C. | 若a⊥α,b⊥α,则a∥b | D. | 若a∥α,b∥α,则a∥b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<$\frac{π}{2}$,tanθ=3$\sqrt{3}$),且与商业中心O的距离为$\sqrt{21}$公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处,当商业中心O到A,B两处的距离之和最小时,A,B的距离为3$\sqrt{3}$公里.
如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<$\frac{π}{2}$,tanθ=3$\sqrt{3}$),且与商业中心O的距离为$\sqrt{21}$公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处,当商业中心O到A,B两处的距离之和最小时,A,B的距离为3$\sqrt{3}$公里.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是梯形,AB∥DC,∠BAD=90°,AB=AD=$\frac{1}{2}$CD=1
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是梯形,AB∥DC,∠BAD=90°,AB=AD=$\frac{1}{2}$CD=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com