
分析 由题意可得,$\left\{\begin{array}{l}{f(0)=b>0}\\{f(1)=1+a+b>0}\\{0<-\frac{a}{2}<1}\\{f(-\frac{a}{2})=\frac{{a}^{2}}{4}-\frac{{a}^{2}}{2}+b<0}\end{array}\right.$,从而作出平面区域,而min{f(0),f(1)}=$\left\{\begin{array}{l}{b,-1≤a<0}\\{1+a+b,-2<a<-1}\end{array}\right.$,从而分类讨论求取值范围即可
解答 解:∵函数f(x)=x2+ax+b在(0,1)上有两个零点,
∴$\left\{\begin{array}{l}{f(0)=b>0}\\{f(1)=1+a+b>0}\\{0<-\frac{a}{2}<1}\\{f(-\frac{a}{2})=\frac{{a}^{2}}{4}-\frac{{a}^{2}}{2}+b<0}\end{array}\right.$,
由题意作平面区域如下,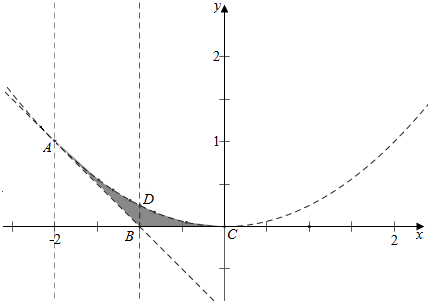 ,
,
∵f(0)=b,f(1)=1+a+b,
∴min{f(0),f(1)}=$\left\{\begin{array}{l}{b,-1≤a<0}\\{1+a+b,-2<a<-1}\end{array}\right.$,
结合图象可知,D(-1,$\frac{1}{4}$),
当-1≤a<0时,0<b<$\frac{1}{4}$,
当-2<a<-1时,0<1+a+b<$\frac{1}{4}$,
综上所述,min{f(0),f(1)}的取值范围是(0,$\frac{1}{4}$);
故答案为:(0,$\frac{1}{4}$).
点评 本题考查了线性规划的变形应用及数形结合、分类讨论的思想应用,同时考查了函数的零点与函数的图象的关系应用.


科目:高中数学 来源: 题型:选择题
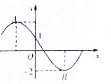 如图所示的函数$f(x)=2sin(wx+φ)(w>0,\frac{π}{2}≤φ≤π)$的部分图象,其中A、B两点之间的距离为5,那么f(-1)=( )
如图所示的函数$f(x)=2sin(wx+φ)(w>0,\frac{π}{2}≤φ≤π)$的部分图象,其中A、B两点之间的距离为5,那么f(-1)=( )| A. | -1 | B. | 2 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{3},1)∪(\sqrt{3},+∞)$ | B. | $(-∞,-1)∪(\sqrt{3},+∞)$ | C. | $(-∞,-\sqrt{3})∪(\sqrt{3},+∞)$ | D. | $(-\sqrt{3},-1)∪(1,\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com