


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
| AD |
| AB |
| AC |
| AB |
| AC |
| AD |
| AC |
| ||
|
|
| AB |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5π |
| 6 |
3
| ||
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,△ABC的三个内角分别为A,B,C,cosA=
如图,△ABC的三个内角分别为A,B,C,cosA=| 1 |
| 3 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-| 1 |
| 2 |
| ||
| 2 |
| OQ |
| OA |
| OP |
| π |
| 6 |
| π |
| 2 |
| OB |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
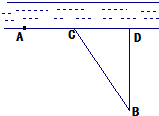 甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com