考点:直线与平面所成的角,平面与平面平行的判定
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(Ⅰ)运用中位线定理和线面平行的判定定理,以及面面平行的判定定理.即可得证;
(Ⅱ)取AB中点D,连接CD,A1D,运用线面垂直的性质和判定定理,即可得到∠CA1D为A1C与平面ABB1A1所成的角,再通过解Rt△CA1D,即可得到所求的角.
解答:
(Ⅰ)证明:∵M,P分别是A
1C
1,A
1C的中点,∴MP∥CC
1,
又CC
1∥AA
1,∴MP∥AA
1,又MP?平面ABB
1A
1,AA
1?平面ABB
1A
1,
∴MP∥平面ABB
1A
1,
同理PN∥平面ABB
1A
1,MP∩PN=P,
∴平面MNP∥平面ABB
1A
1;
(Ⅱ)解:取AB中点D,连接CD,A
1D,
∵AA
1⊥平面ABC,CD?平面ABC,∴AA
1⊥CD,
又∵AC=BC,D为AB中点,∴CD⊥AB,又AA
1∩AB=A,
∴CD⊥平面ABB
1A
1,
∴∠CA
1D为A
1C与平面ABB
1A
1所成的角.
在Rt△CA
1D中,∠CDA
1=90°,设CA=1,可得CD=
,A
1C=
,
sin∠CA
1D=
=
,∴∠CA
1D=30°,
即A
1C与平面ABB
1A
1所成的角为30°.
点评:本题考查空间两平面平行的判定定理和运用,考查空间线面所成角的求法,考查运算能力,属于中档题.

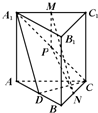
 如图,在直三棱柱A1B1C1-ABC中,∠ACB=90°,CA=CB=CC1,M,P,N分别为A1C1,A1C,BC的中点.
如图,在直三棱柱A1B1C1-ABC中,∠ACB=90°,CA=CB=CC1,M,P,N分别为A1C1,A1C,BC的中点. (Ⅰ)证明:∵M,P分别是A1C1,A1C的中点,∴MP∥CC1,
(Ⅰ)证明:∵M,P分别是A1C1,A1C的中点,∴MP∥CC1,

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案