
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线恰与曲线
处的切线恰与曲线![]() 相切,求a的值;
相切,求a的值;
(2)不等式![]() 对一切正实数x恒成立,求a的取值范围;
对一切正实数x恒成立,求a的取值范围;
(3)已知![]() ,若函数
,若函数![]() 在
在![]() 上有且只有一个零点,求a的取值范围.
上有且只有一个零点,求a的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)求出切线方程后,再与二次函数联立,利用判别式为0,即可求得![]() 的值;
的值;
(2)将问题转化为![]() 对任意的
对任意的![]() 恒成立,再利用参变分离和构造函数,即可得答案;
恒成立,再利用参变分离和构造函数,即可得答案;
(3)由题意得![]() ,
,![]() ,对
,对![]() 分
分![]() 和
和![]() 两种情况讨论,从而求得
两种情况讨论,从而求得![]() 的取值范围.
的取值范围.
(1)因为![]() ,所以
,所以![]() ,又切点为
,又切点为![]() ,
,
因此曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,
,
将![]() 与
与![]() 联立,消去y得:
联立,消去y得:![]() ,
,
由题意知![]() ,
,
解得![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
即![]() ,
,
设![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
因此![]() ,
,
所以![]() ,即
,即![]() .
.
(3)![]() ,
,![]() ,
,
①当![]() 时,
时,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
所以![]() ,
,
当![]() ,即
,即![]() 时,
时,
因为![]() ,
,
又![]() ,
,
所以![]() 在
在![]() 上存在唯一的零点,
上存在唯一的零点,
因此![]() 在
在![]() 上无零点,所以
上无零点,所以![]() 即
即![]() ,解得
,解得![]()
又![]() ,所以
,所以![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 有唯一的零点
有唯一的零点![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 无零点.
无零点.
②当![]() 时,
时,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
因为![]() ,所以当
,所以当![]() ,
,![]() 无零点.
无零点.
设![]() ,则
,则![]() ,于是
,于是![]() ,
,
又![]() ,
,
所以![]() 在
在![]() 上存在唯一的零点,即
上存在唯一的零点,即![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
综上可知,![]() 或
或![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有一个“引葭赴岸”问题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思为“今有水池1丈见方(即![]() 尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设
尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设![]() ,现有下述四个结论:
,现有下述四个结论:
①水深为12尺;②芦苇长为15尺;③![]() ;④
;④![]() .
.
其中所有正确结论的编号是( )
A.①③B.①③④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() .已知方程
.已知方程![]() 在区间
在区间![]() 上所有的实数根之和为
上所有的实数根之和为![]() .将函数
.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则
的图象,则![]() __________,
__________,![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是由CCTV-10自主研发的一档大型文化益智节目,以“赏中华诗词,寻文化基因品生活之美”为宗旨,带动全民重温经典、从古人的智慧和情怀中汲取营养、涵养心灵,节目广受好评还因为其颇具新意的比赛规则:每场比赛,106位挑战者全部参赛,分为单人追逐赛和擂主争霸赛两部分单人追逐赛的最终优胜者作为攻擂者与守擂擂主进行比拼,竞争该场比赛的擂主,擂主争霸赛以抢答的形式展开,共九道题,抢到并回答正确者得一分,答错则对方得一分,先得五分者获胜,成为本场擂主,比赛结束已知某场擂主争霸赛中,攻擂者与守擂擂主都参与每一次抢题且两人抢到每道题的概率都是![]() ,攻擂者与守擂擂主正确回答每道题的概率分别为
,攻擂者与守擂擂主正确回答每道题的概率分别为![]() ,
,![]() ,且两人各道题是否回答正确均相互独立.
,且两人各道题是否回答正确均相互独立.
(1)比赛开始,求攻擂者率先得一分的概率;
(2)比赛进行中,攻擂者暂时以![]() 领先,设两人共继续抢答了
领先,设两人共继续抢答了![]() 道题比赛结束,求随机变量
道题比赛结束,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2y,过点(0,2)作直线l交抛物线于A、B两点.
(1)证明:OA⊥OB;
(2)若直线l的斜率为1,过点A、B分别作抛物线的切线l1,l2,若直线l1,l2,相交于点P,直线l1,l2交x轴分别于点M,N,求△MNP的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,离心率
,离心率![]() ,
,![]() 是椭圆的左顶点,
是椭圆的左顶点,![]() 是椭圆的左焦点,
是椭圆的左焦点,![]() ,直线
,直线![]() :
:![]() .
.
(1)求椭圆![]() 方程;
方程;
(2)直线![]() 过点
过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 分别与直线
分别与直线![]() 交于
交于![]() 、
、![]() 两点,试问:以
两点,试问:以![]() 为直径的圆是否过定点,如果是,请求出定点坐标;如果不是,请说明理由.
为直径的圆是否过定点,如果是,请求出定点坐标;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地在每周六的晚上8点到10点半举行灯光展,灯光展涉及到10000盏灯,每盏灯在某一时刻亮灯的概率均为![]() ,并且是否亮灯彼此相互独立.现统计了其中100盏灯在一场灯光展中亮灯的时长(单位:
,并且是否亮灯彼此相互独立.现统计了其中100盏灯在一场灯光展中亮灯的时长(单位:![]() ),得到下面的频数表:
),得到下面的频数表:
亮灯时长/ |
|
|
|
|
|
频数 | 10 | 20 | 40 | 20 | 10 |
以样本中100盏灯的平均亮灯时长作为一盏灯的亮灯时长.
(1)试估计![]() 的值;
的值;
(2)设![]() 表示这10000盏灯在某一时刻亮灯的数目.
表示这10000盏灯在某一时刻亮灯的数目.
①求![]() 的数学期望
的数学期望![]() 和方差
和方差![]() ;
;
②若随机变量![]() 满足
满足![]() ,则认为
,则认为![]() .假设当
.假设当![]() 时,灯光展处于最佳灯光亮度.试由此估计,在一场灯光展中,处于最佳灯光亮度的时长(结果保留为整数).
时,灯光展处于最佳灯光亮度.试由此估计,在一场灯光展中,处于最佳灯光亮度的时长(结果保留为整数).
附:
①某盏灯在某一时刻亮灯的概率![]() 等于亮灯时长与灯光展总时长的商;
等于亮灯时长与灯光展总时长的商;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家每年都会对中小学生进行体质健康监测,一分钟跳绳是监测的项目之一.今年某小学对本校六年级300名学生的一分钟跳绳情况做了统计,发现一分钟跳绳个数最低为10,最高为189.现将跳绳个数分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6组,并绘制出如下的频率分布直方图.
6组,并绘制出如下的频率分布直方图.
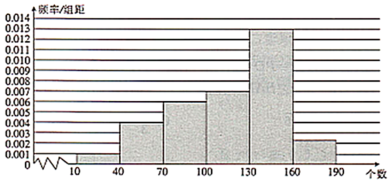
(1)若一分钟跳绳个数达到160为优秀,求该校六年级学生一分钟跳绳为优秀的人数;
(2)上级部门要对该校体质监测情况进行复查,发现每组男、女学生人数比例有很大差别,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() .试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
.试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正整数m,n满足![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为集各
为集各![]() 的n元子集,且
的n元子集,且![]() ;
;
(1)若![]() ,满足
,满足![]() ;
;
(i)求证:![]() ;
;
(ii)求满足条件的集合![]() 的个数;
的个数;
(2)若![]() 中至多有一个元素,求证:
中至多有一个元素,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com