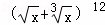练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    展开式中有理项共有　 　 项．


    3.

    【解析】展开式通项公式为Tr+1==

    若为有理项时，则为整数，

    ∴r=0、6、12，故展开式中有理项共有3项，

    故答案为：3


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知f(x)＝Asin(ωx＋φ)(A>0，ω>0)的最小正周期为2，且当x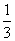＝时，f(x)的最大值为2.

    (1)求f(x)的解析式．

    (2)在闭区间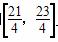上是否存在f(x)的对称轴？如果存在求出其对称轴．若不正在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    以曲线的焦点为圆心，和直线相切的圆的方程为(   )   (第4题)

         A．                 B．

         C．              D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数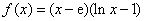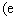为自然对数的底数）．

    （Ⅰ）求曲线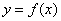在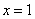处的切线方程；

    （Ⅱ）若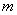是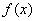的一个极值点，且点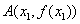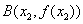，满足条件：

    .

    （ⅰ）求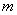的值；

    （ⅱ）求证：点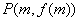，，是三个不同的点，且构成直角三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知F1（﹣c，0），F2（c，0）为椭圆的两个焦点，P为椭圆上一点且，则此椭圆离心率的取值范围是（　　）

    　

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正四棱柱中，.

    （Ⅰ）求证：；

    （Ⅱ）求二面角的余弦值；

    （Ⅲ）在线段上是否存在点，使得平面平面，若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合则 “”是“”的（    ）

    A. 充分不必要条件               B. 必要不充分条件

    C. 充分必要条件                 D. 既不充分又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知二次函数在处取得极值，且在点处的切线与直线平行．   (1）求的解析式；(2）求函数的单调递增区间及极值。（3）求函数在的最值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


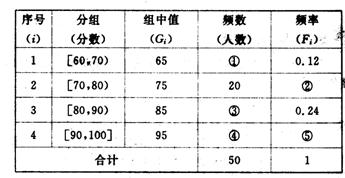
    为了让学生等多的了解“数学史”知识，某中学高二年级举办了一次“追寻先哲的足迹，倾听数学的声音”的数学史知识竞赛活动，共有800名学生参加了这次竞赛，为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，统计结果见下表。请你根据频率分布表解答下列问题：

    （1）填充频率分布表中的空格。

    （2）为鼓励学生更多的学生了解“数学史”知识，成绩不低于85分的同学能获奖，请估计在参加的800名学生中大概有多少名学生获奖？

    （3）在上述统计数据的分析中有一项计算见算法流程图，求输出的S的值.

          

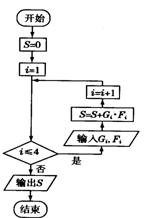
    查看答案和解析>>

    同步练习册答案