
(满分13分)如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为 .
.

(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
(3)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.
(1)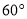 ; (2)
; (2)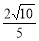 ; (3)F是AD的4等分点,靠近A点的位置.
; (3)F是AD的4等分点,靠近A点的位置.
【解析】
试题分析:(1)取AD中点M,连接MO,PM,由正四棱锥的性质知∠PMO为所求二面角P-AD-O的平面角,∠PAO为侧棱PA与底面ABCD所成的角∴tan∠PAO=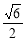 ,设AB=a,则AO=
,设AB=a,则AO=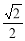 a,PO=
a,PO=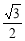 a,MO=
a,MO=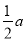 , tan∠PMO=
, tan∠PMO=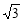 ,∠PMO=60°; (2)依题意连结AE,OE,则OE∥PD ,故∠OEA为异面直线PD与AE所成的角,由正四棱锥的性质易证OA⊥平面POB,故
,∠PMO=60°; (2)依题意连结AE,OE,则OE∥PD ,故∠OEA为异面直线PD与AE所成的角,由正四棱锥的性质易证OA⊥平面POB,故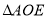 为直角三角形,OE=
为直角三角形,OE=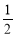 PD=
PD=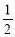
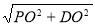 =
=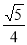 a ∴tan∠AEO=
a ∴tan∠AEO=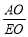 =
=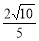 ;(3)延长MO交BC于N,取PN中点G,连BG,EG,MG,易得BC⊥平面PMN,故平面PMN⊥平面PBC,而△PMN为正三角形,易证MG⊥平面PBC,取MA的中点F,连EF,则四边形MFEG为平行四边形,从而MG//FE,EF⊥平面PBC, F是AD的4等分点,靠近A点的位置.
;(3)延长MO交BC于N,取PN中点G,连BG,EG,MG,易得BC⊥平面PMN,故平面PMN⊥平面PBC,而△PMN为正三角形,易证MG⊥平面PBC,取MA的中点F,连EF,则四边形MFEG为平行四边形,从而MG//FE,EF⊥平面PBC, F是AD的4等分点,靠近A点的位置.
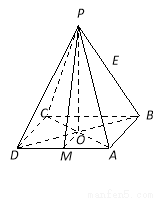
试题解析:(1)取AD中点M,连接MO,PM,依条件可知AD⊥MO,AD⊥PO,则∠PMO为所求二面角P-AD-O的平面角 (2分)
∵PO⊥面ABCD,
∴∠PAO为侧棱PA与底面ABCD所成的角.
∴tan∠PAO=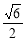
设AB=a,AO=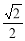 a,
a,
∴ PO=AO·tan∠POA=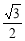 a,
a,
tan∠PMO=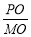 =
=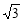 .
.
∴∠PMO=60°. (4分)

(2)连接AE,OE, ∵OE∥PD,
∴∠OEA为异面直线PD与AE所成的角. (6分)
∵AO⊥BD,AO⊥PO,∴AO⊥平面PBD.
又OE 平面PBD, ∴ AO⊥OE.
平面PBD, ∴ AO⊥OE.
∵OE=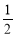 PD=
PD=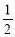
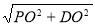 =
=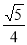 a,
a,
∴tan∠AEO=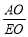 =
=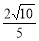 . (8分)
. (8分)
(3)延长MO交BC于N,取PN中点G,连BG,EG,MG.

∵BC⊥MN,BC⊥PN,∴BC⊥平面PMN
∴平面PMN⊥平面PBC. (10分)
又PM=PN,∠PMN=60°,∴△PMN为正三角形.
∴MG⊥PN.又平面PMN ∩平面PBC=PN,∴MG⊥平面PBC. (12分)
 F是AD的4等分点,靠近A点的位置 (13分)
F是AD的4等分点,靠近A点的位置 (13分)
考点:立体几何的综合问题


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源:2014-2015学年湖北襄阳襄州一中等四校高二上学期期中文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知直线 经过两条直线
经过两条直线 和
和 的交点.
的交点.
(1)若直线 平行于直线
平行于直线 ,求直线
,求直线 的方程;
的方程;
(2)若直线 垂直于直线
垂直于直线 ,求直线
,求直线 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北襄阳襄州一中等四校高二上学期期中文科数学试卷(解析版) 题型:选择题
已知二次函数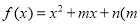 、
、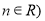 的两个零点分别在
的两个零点分别在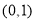 与
与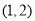 内,则
内,则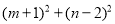 的取值范围是( )
的取值范围是( )
A.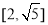 B.
B.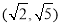 C.
C.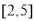 D.
D.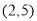
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北襄阳襄州一中等四校高二上学期期中文科数学试卷(解析版) 题型:选择题
用“除 取余法”将十进制数
取余法”将十进制数 转化为五进制数是( )
转化为五进制数是( )
A. B.
B. C.
C.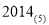 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北襄州一中等四校高二上学期期中联考理科数学试卷(解析版) 题型:选择题
如图甲所示,三棱锥 的高
的高 ,
, ,
, ,M、N分别在
,M、N分别在 和
和 上,且
上,且 ,
, ,图乙中的四个图像大致描绘了三棱锥
,图乙中的四个图像大致描绘了三棱锥 的体积y与
的体积y与 的变化关系,其中正确的是( )
的变化关系,其中正确的是( )

查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
设随机变量ξ~N(0,1),若P(ξ>1)=p,则P(﹣1<ξ<0)= _________ .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试文科数学试卷(解析版) 题型:填空题
某人有4把钥匙, 其中2把能打开门, 现随机地取1把钥匙试着开门, 不能开门就把钥匙放在旁边, 他第二次才能打开门的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com