
 如图,在直三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E是CC1上的中点,且BC=1,BB1=2.
如图,在直三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E是CC1上的中点,且BC=1,BB1=2.分析 (Ⅰ)连接BE,只需证明BE⊥B1E,且AB⊥B1E=B,即可得到B1E⊥平面ABE;
(Ⅱ)由V${\;}_{A-BE{A}_{1}}$=V${\;}_{{A}_{1}-ABE}$=V${\;}_{{B}_{1}ABE}$=$\frac{1}{3}×{s}_{△ABE}×{B}_{1}E$=$\frac{1}{3}×\frac{1}{2}×AB×BE×{B}_{1}E=\frac{\sqrt{3}}{3}$,得AB=$\sqrt{3}$,异面直线AB和A1C1所成角为∠CAB,即可求解.
解答 证明:(Ⅰ)连接BE,∵BC=1 BB1=2,E是CC1上的中点
△BCE,△B1C1E为等腰直角三角形,即$∠BEC=∠{B}_{1}E{C}_{1}=\frac{π}{4}$,∴$∠BE{B}_{1}=\frac{π}{2}$,即BE⊥B1E
∵AB⊥面BB1C1C.B1E?面ABC,∴B1E⊥AB,且AB∩BE=B,
∴B1E⊥平面ABE;
解:(Ⅱ)∵AB∥A1B1,∴A1、B1到面ABE的距离相等,
由(Ⅰ)得BE=B1E=$\sqrt{2}$
故V${\;}_{A-BE{A}_{1}}$=V${\;}_{{A}_{1}-ABE}$=V${\;}_{{B}_{1}ABE}$
=$\frac{1}{3}×{s}_{△ABE}×{B}_{1}E$=$\frac{1}{3}×\frac{1}{2}×AB×BE×{B}_{1}E=\frac{\sqrt{3}}{3}$
解得AB=$\sqrt{3}$
∵AC∥A1C1,∴异面直线AB和A1C1所成角为∠CAB,
在Rt△ABC中,tan$∠CAB=\frac{CB}{AB}=\frac{\sqrt{3}}{3}$,∴∠CAB=30°
∴异面直线AB和A1C1所成角的大小30°.
点评 本题考查了空间线面垂直的判定,考查了异面直线夹角的求法,属于中档题.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某市有6条南北向街道,4条东西向街道,图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )
某市有6条南北向街道,4条东西向街道,图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )| A. | m=90,n=56 | B. | m=30,n=56 | C. | m=90,n=792 | D. | m=30,n=792 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
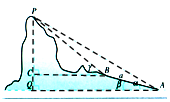 如图,在山脚A测得山顶P的仰角为60°,沿倾斜角为15°的斜坡向上走200米到B,在B处测得山顶P的仰角为75°,则山高h=150($\sqrt{6}$+$\sqrt{2}$)米.
如图,在山脚A测得山顶P的仰角为60°,沿倾斜角为15°的斜坡向上走200米到B,在B处测得山顶P的仰角为75°,则山高h=150($\sqrt{6}$+$\sqrt{2}$)米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{π}{2})<f(\frac{4π}{3})<f(\frac{π}{12})$ | B. | f($\frac{π}{12}$)<f($\frac{π}{2}$)<f($\frac{4π}{3}$) | C. | $f(\frac{π}{2})<f(\frac{π}{12})<f(\frac{4π}{3})$ | D. | $f(\frac{π}{12})<f(\frac{4π}{3})<f(\frac{π}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (3,4) | C. | (1,3) | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 我国齐梁时代的数学家祖暅(公元前5-6世纪,祖冲之之子)提出了一条原理:“幂势既同,则积不容异”,这个原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体,如图,将底面直径都为2b,高皆为a的椭半球体和已被挖去了圆锥体的圆柱体放置于同一平面β上,用平行于平面β且与平面β任意距离d处的平面截这两个几何体,可横截得到S圆及S环两截面,可以证明S圆=S环总成立.据此,短轴长为$2\sqrt{3}$,长轴为5的椭球体的体积是10π.
我国齐梁时代的数学家祖暅(公元前5-6世纪,祖冲之之子)提出了一条原理:“幂势既同,则积不容异”,这个原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体,如图,将底面直径都为2b,高皆为a的椭半球体和已被挖去了圆锥体的圆柱体放置于同一平面β上,用平行于平面β且与平面β任意距离d处的平面截这两个几何体,可横截得到S圆及S环两截面,可以证明S圆=S环总成立.据此,短轴长为$2\sqrt{3}$,长轴为5的椭球体的体积是10π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com