
【题目】定义在![]() 上的函数
上的函数![]() 满足:对任意的
满足:对任意的![]() ,都有:
,都有:![]()
(1)求证:函数![]() 是奇函数;
是奇函数;
(2)若当![]() 时,有
时,有![]() ,求证:
,求证:![]() 在
在![]() 上是减函数;
上是减函数;
(3)在(2)的条件下解不等式:![]() ;
;
(4)在(2)的条件下求证:![]() .
.
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上![]() 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() , ,
, ,![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
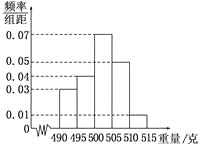
(1)根据频率分布直方图,求重量超过![]() 克的产品数量;
克的产品数量;
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列;
的分布列;
(3)从该流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 有以下性质:
有以下性质:
①过圆![]() 上一点
上一点![]() 的圆的切线方程是
的圆的切线方程是![]() .
.
②若不在坐标轴上的点![]() 为圆
为圆![]() 外一点,过
外一点,过![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,则
,则![]() 垂直
垂直![]() ,即
,即![]() .
.
(1)类比上述有关结论,猜想过椭圆![]() 上一点
上一点![]() 的切线方程 (不要求证明);
的切线方程 (不要求证明);
(2)若过椭圆![]() 外一点
外一点![]() (
(![]() 不在坐标轴上)作两直线,与椭圆相切于
不在坐标轴上)作两直线,与椭圆相切于![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,且它的离心率与双曲线
,且它的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆的方程;
(2)过点A且斜率为k的直线l与椭圆相交于A,B两点,点M在椭圆上,且满![]() 求k的值.
求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是中华人民共和国成立70周年,某校党支部举办了一场“我和我的祖国”知识竞赛,满分100分,回收40份答卷,成绩均落在区间![]() 内,将成绩绘制成如下的频率分布直方图.
内,将成绩绘制成如下的频率分布直方图.
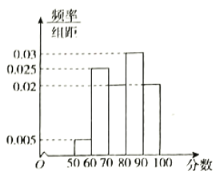
(1)估计知识竞赛成绩的中位数和平均数;
(2)从![]() ,
,![]() 分数段中,按分层抽样随机抽取5份答卷,再从对应的党员中选出3位党员参加县级交流会,求选出的3位党员中有2位成绩来自于
分数段中,按分层抽样随机抽取5份答卷,再从对应的党员中选出3位党员参加县级交流会,求选出的3位党员中有2位成绩来自于![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() 的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
(1)若直线AP与BP的斜率之积为 ![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|> ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com