
分析 换元法,设t=sinx+cosx,由三角函数知识可得t∈[-$\sqrt{2}$,$\sqrt{2}$],且sin2x=t2-1,可得f(x)=m(sinx+cosx)+sin2x=mt+t2-1,由二次函数区间的最值可得.
解答 解:设t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],
∴t2=(sinx+cosx)2=1+sin2x,
∴sin2x=t2-1,
∴f(x)=m(sinx+cosx)+sin2x=mt+t2-1=(t-$\frac{m}{2}$)2-$\frac{1}{4}{m}^{2}$-1,
当$\frac{m}{2}$≤0时,即m≤0时,此时f(x)max=f($\sqrt{2}$)=1+$\sqrt{2}$m,
当$\frac{m}{2}$>0时,即m>0时,此时f(x)max=f(-$\sqrt{2}$)=1-$\sqrt{2}$m,
故f(x)max=$\left\{\begin{array}{l}{1+\sqrt{2}m,m≤0}\\{1-\sqrt{2}m,n>0}\end{array}\right.$.
点评 本题考查三角函数的值域,涉及换元法和三角函数的值域以及二次函数区间的最值,属中档题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
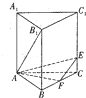 如图,直三棱柱ABC-A1B1C1的棱长均相等,点F为棱BC的中点,点E在棱CC1上,且EF⊥AB1.
如图,直三棱柱ABC-A1B1C1的棱长均相等,点F为棱BC的中点,点E在棱CC1上,且EF⊥AB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7或$\frac{1}{7}$ | B. | 5或$\frac{1}{5}$ | C. | 3或$\frac{1}{3}$ | D. | e或$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com