
| A. | 7或$\frac{1}{7}$ | B. | 5或$\frac{1}{5}$ | C. | 3或$\frac{1}{3}$ | D. | e或$\frac{1}{e}$ |
分析 将t换为t+2,可得f(t+4)=f(t),可得f(x)为最小正周期为4的函数;再由奇函数的定义可得f(t+2)=f(-t),则函数f(x)的图象关于直线x=1对称,求得[0,1]时f(x)的单调性,画出f(x)的图象,由题意可得函数y=f(x)的图象和函数y=loga|x|的图象有5个交点,讨论a>1,0<a<1时,函数的图象的交点情况,即可得到a的取值.
解答 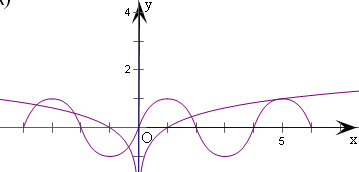 解:任意t∈R都有f(2+t)+f(t)=0,
解:任意t∈R都有f(2+t)+f(t)=0,
即为f(t+2)=-f(t),
t换为t+2,可得f(t+4)=-f(t+2)=f(t),
可得f(x)为最小正周期为4的函数;
又f(-t)=-f(t),即有f(t+2)=f(-t),
则函数f(x)的图象关于直线x=1对称,
由x∈[0,1]时,f(x)=$\frac{ex}{{e}^{x}}$,
f′(x)=$\frac{e-ex}{{e}^{x}}$,可得(0,1)为f(x)的增区间,
由f(x)的对称性和周期性,画出y=f(x)的图象,
由函数g(x)=f(x)-loga|x|在其定义域上有5个零点,
即为函数y=f(x)的图象和函数y=loga|x|的图象有5个交点,
当a>1时,如图可得,x>0时,x=5时,f(5)=f(1)=1,
由loga5=1,解得a=5,且f(x)的值域为[-1,1],
显然当x>5时,y=f(x)的图象和函数y=log5x的图象没有交点,
即x>0时,y=f(x)的图象和函数y=log5x的图象有2个交点;
x<0时,y=f(x)的图象和函数y=log5|x|的图象有3个交点,
同理可得,a=$\frac{1}{5}$时,x>0时,y=f(x)的图象和函数y=loga|x|的图象有3个交点,
x<0时,y=f(x)的图象和函数y=loga|x|的图象有2个交点.
综上可得,当a=5或$\frac{1}{5}$时,函数g(x)=f(x)-loga|x|在其定义域上有5个零点.
故选:B.
点评 本题考查函数的零点个数问题的解法,注意运用转化思想和分类讨论的思想方法,以及数形结合的方法,考查观察能力和判断能力,正确画出函数的图象是解题的关键,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,且椭圆C上一点M与椭圆左右两个焦点构成的三角形周长为4+2$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,且椭圆C上一点M与椭圆左右两个焦点构成的三角形周长为4+2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
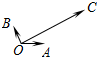 如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).
如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log23 | B. | 0 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某几何体的正视图和侧视图如图(1)所示,它的俯视图的直观图是△A′B′C′,如图(2)所示,其中O′A′=O′B′=2,O′C′=$\sqrt{3}$,则该几何体的外接球的表面积为$\frac{112π}{3}$.
某几何体的正视图和侧视图如图(1)所示,它的俯视图的直观图是△A′B′C′,如图(2)所示,其中O′A′=O′B′=2,O′C′=$\sqrt{3}$,则该几何体的外接球的表面积为$\frac{112π}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com