
分析 (1)利用已知条件列出不等式求解即可.
(2)利用二次函数的性质,通过配方求解函数的最值即可.
解答 解:(1)根据题意,
有$100(5x-\frac{3}{x}+1)≥1500$,
得5x2-14x-3≥0,得x≥3或$x≤-\frac{1}{5}$,
又1≤x≤10,得3≤x≤10.
(2)生产480千克该产品获得的利润为$u=24000(5+\frac{1}{x}-\frac{3}{x^2})$,1≤x≤10,
记$f(x)=-\frac{3}{x^2}+\frac{1}{x}+5$,1≤x≤10,
则$f(x)=-3{(\frac{1}{x}-\frac{1}{6})^2}+\frac{1}{12}+5$
当且仅当x=6时取得最大值$\frac{61}{12}$,
则获得的最大利润为$u=24000×\frac{61}{12}=122000$(元)
故该厂以6千克/小时的速度生产,可获得最大利润为122000元.
点评 本题考查函数的实际应用,二次函数的性质,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | l | C. | -l | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )| A. | i≤1009 | B. | i>1009 | C. | i≤1010 | D. | i>1010 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:填空题
若数列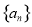 满足
满足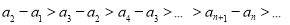 ,则称数列
,则称数列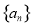 为“差递减”数列.若数列
为“差递减”数列.若数列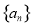 是“差递减”数列,且其通项
是“差递减”数列,且其通项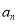 与其前
与其前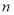 项和
项和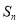 (
( )满足
)满足 (
( ),则实数
),则实数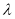 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈(0,+∞),lnx0≠2x0+1 | B. | ?x0∉(0,+∞),lnx0=2x0+1 | ||
| C. | ?x∈(0,+∞),lnx≠2x+1 | D. | ?x∉(0,+∞),lnx≠2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com