
分析 (1)根据函数的定义域为R,关于原点对称,且满足f(-x)=f(x),可得函数 f(x)是偶函数.
(2)先去绝对值,然后根据二次函数、分段函数图象的画法画出函数f(x)的图象.
(3)通过图象即可求得f(x)的单调递增和递减区间;
(4)通过图象即可得到k的取值和对应的原方程实根的个数.
解答 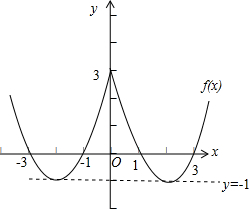 解:(1)由于函数f(x)=x2-4|x|+3的定义域为R,
解:(1)由于函数f(x)=x2-4|x|+3的定义域为R,
关于原点对称,
且满足f(-x)=(-x)2-4|-x|+3=x2-4|x|+3=f(x),
故函数 f(x)是偶函数.
(2)f(x)的图象如图所示:
(3)根据图象指出函数f(x)的单调递增区间
为[-2,0]、[2,+∞);
单调递减区间为(-∞,-2]、[0,2].
(4)当实数k取不同的值时,
讨论关于x的方程x2-4|x|+3=k的实根的个数,
即函数y=x2-4|x|+3的图象和直线y=k交点的个数.
由图象可看出,当k<-1时,方程实根的个数为0;
当k=-1时,方程实根的个数为2;
当-1<k<3时,方程实根个数为4;
当k=3时,方程实根个数为3;
当k>3时,方程实根个数为2.
点评 本题主要考查含绝对值函数的处理方法:去绝对值,二次函数、分段函数图象的画法,函数单调性的定义,以及根据图象写出函数的单调区间,数形结合讨论方程实根个数的方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
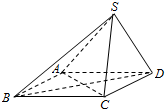 已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.
已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
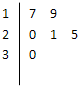 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com