Question

6．已知直三棱柱ABC-A₁B₁C₁的各顶点都在半径为$\sqrt{5}$的球面上，且边AB=AC=1，BC=$\sqrt{2}$，则这个直三棱柱的体积等于（　　）

• A． $\frac{3\sqrt{2}}{2}$
• B． $\sqrt{3}$
• C． $\frac{\sqrt{2}}{2}$
• D． $\sqrt{5}$

Answer 1

分析 如图所示，分别取BC，B₁C₁的中点D，D₁，连接DD₁，设DD₁的中点为O，由边AB=AC=1，BC=$\sqrt{2}$，可得AB⊥AC，因此点D为△ABC的外心，可得DA=DB=DC．可得DD₁⊥平面ABC，且点O到各个顶点的距离相等，则点O为外接球的球心．可得OD，利用直三棱柱的体积=S_△ABC•DD₁即可得出．

解答 解：如图所示，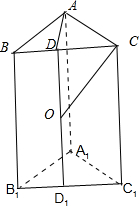
分别取BC，B₁C₁的中点D，D₁，
连接DD₁，设DD₁的中点为O，
∵边AB=AC=1，BC=$\sqrt{2}$，
∴AB⊥AC，
∴点D为△ABC的外心．
DA=DB=DC．
∵DD₁⊥平面ABC，且点O到各个顶点的距离相等，
则点O为外接球的球心．
∴OC²=OD²+CD²，
∴$（\sqrt{5}）^{2}=O{D}^{2}$+$（\frac{\sqrt{2}}{2}）^{2}$，
∴OD=$\frac{3\sqrt{2}}{2}$，
∴DD₁=$3\sqrt{2}$．
∴这个直三棱柱的体积=S_△ABC•DD₁=$\frac{1}{2}×{1}^{2}×3\sqrt{2}$=$\frac{3\sqrt{2}}{2}$．
故选：A．

点评 本题考查了直三棱柱的体积计算公式、球的性质、线面垂直的判定及其性质、勾股定理的逆定理、直角三角形的性质，考查了推理能力与计算能力，属于中档题．