
分析 (1)求导数,确定切线的斜率,即可求f(x)在(1,f(1))处的切线方程;
(2)问题转化为a>x(1-lnx)对x∈(0,2e]恒成立.,求出右边的最大值,即可求实数a的取值范围.
解答 解:(1)a=2时,$f(x)=\frac{2}{x}+lnx-1$,所以$f'(x)=-\frac{2}{x^2}+\frac{1}{x}$,
则f'(1)=-1,又f(1)=1,
所以切线方程为y-1=-(x-1),即x+y-2=0.
(2)因为a>0,且对x∈(0,2e]时,f(x)>0恒成立,
即$\frac{a}{x}+lnx-1>0$对x∈(0,2e]很成立,所以a>x(1-lnx)对x∈(0,2e]恒成立.
设g(x)=x(1-lnx)=x-xlnx,x∈(0,2e],
则g'(x)=1-lnx-1=-lnx,
当0<x<1时,g'(x)>0,g(x)为增函数;
当1<x≤e时,g'(x)<0,g(x)为减函数;
所以g(x)max=g(1)=1-ln1=1,
则实数a的取值范围是(1,+∞).
点评 本题考查导数的几何意义,考查函数的最值,考查构造法的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
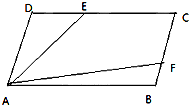 在平行四边形ABCD中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,E、F分别是边CD和BC上的点,满足$\overrightarrow{DC}$=3$\overrightarrow{DE}$,$\overrightarrow{BC}$=3$\overrightarrow{BF}$.
在平行四边形ABCD中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,E、F分别是边CD和BC上的点,满足$\overrightarrow{DC}$=3$\overrightarrow{DE}$,$\overrightarrow{BC}$=3$\overrightarrow{BF}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
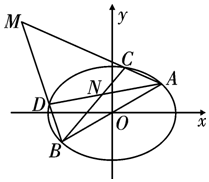 如图,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点A($\sqrt{2}$,1)是椭圆上的一点,且椭圆C的离心率为$\frac{{\sqrt{2}}}{2}$,直线AO与椭圆C交于点B,且C,D是椭圆上异于A,B的任意两点,直线AC,BD相交于点M,直线AD,BC相交于点N.
如图,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点A($\sqrt{2}$,1)是椭圆上的一点,且椭圆C的离心率为$\frac{{\sqrt{2}}}{2}$,直线AO与椭圆C交于点B,且C,D是椭圆上异于A,B的任意两点,直线AC,BD相交于点M,直线AD,BC相交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线和直线外一点确定一个平面 | |
| B. | 过不在一条直线上的三点,有且只有一个平面 | |
| C. | 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补 | |
| D. | 平行于同一个平面的两个平面相互平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | $2\sqrt{2}-i$ | D. | $-2\sqrt{2}+i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com