
已知函数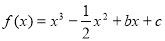
(1)若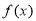 在
在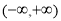 上是增函数,求
上是增函数,求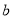 的取值范围;
的取值范围;
(2)若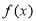 在
在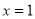 处取得极值,且
处取得极值,且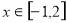 时,
时,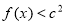 恒成立,求
恒成立,求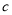 的取值范围.
的取值范围.
(1)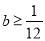 ;(2)(-∞,-1)∪(2,+∞).
;(2)(-∞,-1)∪(2,+∞).
【解析】
试题分析:
解题思路:(1)利用“若函数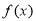 在某区间上单调递增,则
在某区间上单调递增,则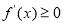 在该区间恒成立”求解;
在该区间恒成立”求解;
(2)先根据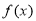 在
在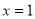 处取得极值求得
处取得极值求得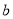 值,再将恒成立问题转化为求
值,再将恒成立问题转化为求 ,解关于
,解关于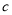 的不等式即可.
的不等式即可.
规律总结:若函数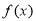 在某区间上单调递增,则
在某区间上单调递增,则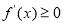 在该区间恒成立;“若函数
在该区间恒成立;“若函数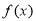 在某区间上单调递减,则
在某区间上单调递减,则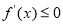 在该区间恒成立;求函数最值的步骤:①
在该区间恒成立;求函数最值的步骤:① 求导函数;②求极值;③比较极值与端点值,得出最值.
求导函数;②求极值;③比较极值与端点值,得出最值.
试题解析:(1)
因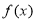 在
在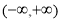 上是增函数,则f′(x)≥0,即3x2-x+b≥0,
上是增函数,则f′(x)≥0,即3x2-x+b≥0,
∴b≥x-3x2在(-∞,+∞)恒成立.
设g(x)=x-3x2,当x=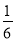 时,g(x)max=
时,g(x)max=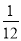 ,∴b≥
,∴b≥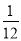 .
.
(2)由题意,知f′(1)=0,即3-1+b=0,∴b=-2.
x∈[-1,2]时,f(x)<c2恒成立,只需f(x)在[-1,2]上的最大值小于c2即可
因f′(x)=3x2-x-2,
令f′(x)=0,得x=1,或x=- .
.
∵f(1)=-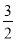 +c,f(-
+c,f(-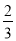 )=
)=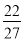 +c,f(-1)=
+c,f(-1)=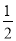 +c,f(2)=2+c,
+c,f(2)=2+c,
∴f(x)max=f(2)=2+c,
∴2+c<c2,解得c>2,或c<-1,
所以c的取值范围为(-∞,-1)∪(2,+∞).
考点:1.函数的单调性;2.函数的极值、最值;3.不等式恒成立问题.


科目:高中数学 来源:2015届福建省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
记者要为5名志愿都和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有 种(用数字作答)
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知函数f(x)=x3+bx2+cx+d(b、c、d为常数),当x∈(0,1)时取得极大值,当x∈(1,2)时取极小值,则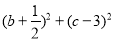 的取值范围是( ).
的取值范围是( ).
A. B.
B. C.
C. D.(5,25)
D.(5,25)
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
在二项式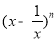 的展开式中恰好第5项的二项式系数最大,则展开式中含
的展开式中恰好第5项的二项式系数最大,则展开式中含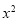 项的系数是( ).
项的系数是( ).
A.-56 B.-35 C.35 D.56
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期末考理科数学试卷(解析版) 题型:填空题
我们把形如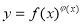 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得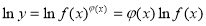 ,两边对x求导数,得
,两边对x求导数,得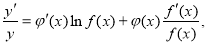 于是
于是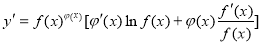 ,
,
运用此方法可以求得函数 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com