
分析 (1)运用椭圆的定义和a,b,c的关系,可得a=2,b=1,进而得到椭圆方程;
(2)求出直线AC的方程,将直线y=kx(k>0)与曲线E联立,求得B,D的坐标,运用点到直线的距离公式,求得B,D到直线AC的距离,再由三角形的面积公式结合基本不等式,即可求得四边形ABCD的面积的最大值.
解答 解:(1)由椭圆的定义可知,曲线E是以F1,F2为焦点的椭圆,
且2a=4,即a=2,
c=$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{4-3}$=1,
即有曲线E的方程为$\frac{{y}^{2}}{4}$+x2=1;
(2)连接AC,直线AC:x+$\frac{y}{2}$=1,即2x+y-2=0,
由y=kx代入椭圆方程可得,x=$±\frac{2}{\sqrt{4+{k}^{2}}}$,
即有B($\frac{2}{\sqrt{4+{k}^{2}}}$,$\frac{2k}{\sqrt{4+{k}^{2}}}$),D(-$\frac{2}{\sqrt{4+{k}^{2}}}$,-$\frac{2k}{\sqrt{4+{k}^{2}}}$),
B到AC的距离为d1=$\frac{|\frac{4}{\sqrt{4+{k}^{2}}}+\frac{2k}{\sqrt{4+{k}^{2}}}-2|}{\sqrt{5}}$=$\frac{2|2+k-\sqrt{4+{k}^{2}}|}{\sqrt{5}•\sqrt{4+{k}^{2}}}$,
D到AC的距离为d2=$\frac{2|2+k+\sqrt{4+{k}^{2}}|}{\sqrt{5}•\sqrt{4+{k}^{2}}}$.
则四边形ABCD面积S=$\frac{1}{2}$|AC|•(d1+d2)=$\frac{1}{2}$$•\sqrt{5}$•$\frac{4(2+k)}{\sqrt{5}•\sqrt{4+{k}^{2}}}$
=$\frac{2(2+k)}{\sqrt{4+{k}^{2}}}$=2$\sqrt{1+\frac{4}{k+\frac{4}{k}}}$≤2$\sqrt{1+\frac{4}{2\sqrt{4}}}$=2$\sqrt{2}$.
当且仅当k=2取得等号.
即四边形ABCD面积的最大值为2$\sqrt{2}$.
点评 本题考查椭圆的方程和性质,主要考查椭圆方程和直线方程联立求交点,同时考查点到直线的距离公式的运用和基本不等式的运用,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:高中数学 来源: 题型:解答题
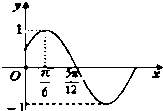 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,令${a_n}=f(\frac{nπ}{6})$,则a1+a2+a3+…+a2014=0.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,令${a_n}=f(\frac{nπ}{6})$,则a1+a2+a3+…+a2014=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80种 | B. | 120种 | C. | 140种 | D. | 50种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com