
分析 (Ⅰ)当b=2时,求导函数,根据函数y=f(x)存在单调递减区间,所以f′(x)<0有解,又因为x>0时,则ax2+2x-1>0有x>0的解,分类讨论,即可求得a的取值范围;
(Ⅱ)设则t1=m+x,t2=m-x,则t1+t2=2m,t1-t2=2x,利用做差法,得到f(m+x)-f(m-x)=mln$\frac{m+x}{m-x}$-2x,构造函数$g(x)=mln\frac{m+x}{m-x}-2x$,利用函数的单调性即可证明;
(Ⅲ)设点A,B的坐标分别是(x1,0),(x2,0),0<x1<x2,利用(Ⅰ)(Ⅱ)即可证明.
解答 解:(Ⅰ)f(x)的定义域为(0,+∞),
∴$f'(x)=\frac{m}{x}-2x+2m-1=-\frac{(2x+1)(x-m)}{x}$,
当m≤0时,f(x)在(0,+∞)上单调递减;
当m>0时,若x∈(0,m),则f'(x)>0,f(x)单调递增,
若x∈(m,+∞),则f'(x)<0,f(x)单调递减,
(Ⅱ)设则t1=m+x,t2=m-x,则t1+t2=2m,t1-t2=2x,
∴f(t1)-f(t2)=mln$\frac{{t}_{1}}{{t}_{2}}$-(t1-t2)(t1+t2)+(2m-1)(t1-t2)=mln$\frac{m+x}{m-x}$-2x,
∴f(m+x)-f(m-x)=mln$\frac{m+x}{m-x}$-2x,
设$g(x)=mln\frac{m+x}{m-x}-2x$,
则$g'(x)=\frac{{2{m^2}}}{{{m^2}-{x^2}}}$,且m>0,0<x<m,
∴g'(x)>0,g(x)在(0,m)上递增,
∴g(x)>g(0)=m>0,
∴f(m+x)>f(m-x).
(Ⅲ)设A,B的横坐标分别为x1,x2,且x1<x2则x1+x2=2x0
由(Ⅰ)可知m>0,且0<x1<m<x2,
由(Ⅱ)可得f(2m-x1)=f(m+(m-x1))>f(m-(m-x1))=f(x1)=f(x2)=0,
又∵f(x)在(m,+∞)上单调递减,
∴2m-x1<x2即2m<x1+x2=2x0?m<x0
由(Ⅰ)f'(x0)<0.
点评 本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,考查学生分析解决问题的能力,有一定的难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
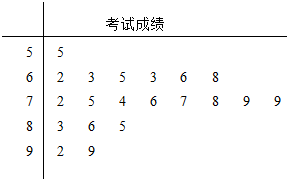
| A. | 74.5 | B. | 75 | C. | 75.5 | D. | 76 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.
如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com