
分析 (1)求出导函数,据导函数的符号与函数单调性的关系,令导函数大于等于0恒成立,分离出a,利用基本不等式求出函数的最小值,令a小于等于最小值即可得到a的范围.
(2)通过函数将函数转化为二次函数,通过对对称轴与定义域位置关系的讨论,分情况求出函数的最小值.
解答 解:(1)f′(x)=2x+$\frac{1}{x}$-a,
∵f(x)在(0,1)上是增函数,
∴2x+$\frac{1}{x}$-a≥0在(0,1)上恒成立,
即a≤2x+$\frac{1}{x}$恒成立,
∴只需a≤(2x+$\frac{1}{x}$)min即可.
∴2x+$\frac{1}{x}$≥2$\sqrt{2}$(当且仅当2x=$\frac{1}{x}$,即x=$\frac{\sqrt{2}}{2}$时取等号),
∴a≤2$\sqrt{2}$;
(2)设ex=t,∵x∈[0,ln3],∴t∈[1,3].
设h(t)=t2-at-1=(t-$\frac{a}{2}$)2-1-$\frac{{a}^{2}}{4}$,
其对称轴t=$\frac{a}{2}$,由(1)得a$≤2\sqrt{2}$,
∴t=$\frac{a}{2}$$≤\sqrt{2}$<$\frac{3}{2}$,
则当1≤$\frac{a}{2}$$≤\sqrt{2}$,即2≤a≤2$\sqrt{2}$时,h(t)的最小值为h($\frac{a}{2}$)=-1-$\frac{{a}^{2}}{4}$;
当$\frac{a}{2}$<1,即a<2时,h(t)的最小值为h(1)=-a
所以,当2$≤a≤2\sqrt{2}$时,g(x)的最小值为-1-$\frac{{a}^{2}}{4}$,
当a<2时,g(x)的最小值为-a.
点评 解决函数的单调性已知求参数的范围问题,常求出导函数,令导函数大于等于(或小于等于)0恒成立;解决不等式恒成立问题常分离参数转化为求函数的最值;通过换元法解题时,一定注意新变量的范围.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
 如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )
如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | A?B | C. | B?A | D. | A=B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
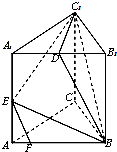 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com