
【题目】试比较3-![]() 与
与![]() (n为正整数)的大小,并予以证明.
(n为正整数)的大小,并予以证明.
【答案】见解析
【解析】
利用作差法可得3-![]() -
-![]() =
=![]() ,确定3-
,确定3-![]() 与
与![]() 的大小关系等价于比较
的大小关系等价于比较![]() 与2n+1的大小,利用数学归纳法证明即可.
与2n+1的大小,利用数学归纳法证明即可.
证明:3-![]() -
-![]() =
=![]() ,
,
于是确定3-![]() 与
与![]() 的大小关系等价于比较
的大小关系等价于比较![]() 与2n+1的大小.
与2n+1的大小.
由2<2×1+1,![]() <2×2+1,
<2×2+1,![]() >2×3+1,
>2×3+1,![]() >2×4+1,
>2×4+1,![]() >2×5+1,
>2×5+1,
可猜想当n≥3时,![]() >2n+1,
>2n+1,
证明如下:
ⅰ当n=3时,由上可知显然成立.
ⅱ假设当n=k时,![]() >2k+1成立.
>2k+1成立.
那么,当n=k+1时,
![]() =2×
=2×![]() >2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1,
>2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1,
所以当n=k+1时猜想也成立,
综合ⅰ和ⅱ,对一切n≥3的正整数,都有![]() >2n+1.
>2n+1.
所以当n=1,2时,3-![]() <
<![]() ;
;
当n≥3时,3-![]() >
>![]() (n为正整数).
(n为正整数).


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(江淮十校2017届高三第一次联考文数试题第7题)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式为:弧田面积=1/2(弦![]() 矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,半径等于4米的弧田.按照上述方法计算出弧田的面积约为( )
,半径等于4米的弧田.按照上述方法计算出弧田的面积约为( )

A. 6平方米 B. 9平方米 C. 12平方米 D. 15平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“圆材埋壁”是《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,学会一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知道大小,用锯取锯它,锯口深一寸,锯道长一尺,问这块圆柱形木材的直径是多少?现有圆柱形木材一部分埋在墙壁中,截面如图所示,已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,则阴影部分面积约为(注:
寸,则阴影部分面积约为(注:![]() ,
,![]() ,1尺=10寸)( )
,1尺=10寸)( )

A. 6.33平方寸B. 6.35平方寸
C. 6.37平方寸D. 6.39平方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.
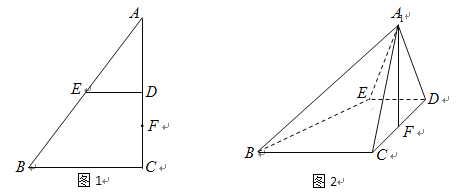
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com