
分析 (1)求出${f}^{'}(x)=\frac{1}{x}-\frac{a}{(x+1)^{2}}$=$\frac{{x}^{2}+(2-a)x+1}{x(x+1)^{2}}$,由题意f′(x)=0在(1,2)上只有一个根,从而f′(1)•f′(2)<0,由此能求出a的取值范围.
(2)推导出$\frac{g({x}_{2})+{x}_{2}-[g({x}_{1})+{x}_{1}]}{{x}_{2}-{x}_{1}}$<0,设h(x)=g(x)+x,则y=h(x)在(0,2]上是减函数,由此利用导数性质能求出a的取值范围.
解答 解:(1)∵函数φ(x)=$\frac{a}{x+1}$,a>0,函数f(x)=lnx+φ(x),
∴${f}^{'}(x)=\frac{1}{x}-\frac{a}{(x+1)^{2}}$=$\frac{{x}^{2}+(2-a)x+1}{x(x+1)^{2}}$,
∵函数f(x)=lnx+φ(x)在(1,2)上只有一个极值点,
∴f′(x)=0在(1,2)上只有一个根,
∵x>0,∴f′(1)•f′(2)=$\frac{1+2-a+1}{1×(1+1)^{2}}$×$\frac{4+(2-a)×2+1}{2(2+1)^{2}}$<0,
解得4<a<$\frac{9}{2}$,
∴a的取值范围是(4,$\frac{9}{2}$).
(2)∵$\frac{g({x}_{2})-g({x}_{1})}{{x}_{2}-{x}_{1}}$<-1,∴$\frac{g({x}_{2})-g({x}_{1})}{{x}_{2}-{x}_{1}}$+1<0,
∴$\frac{g({x}_{2})+{x}_{2}-[g({x}_{1})+{x}_{1}]}{{x}_{2}-{x}_{1}}$<0,
设h(x)=g(x)+x,则y=h(x)在(0,2]上是减函数,
当1<x≤2时,h(x)=lnx+$\frac{a}{x+1}$+x,${h}^{'}(x)=\frac{1}{x}-\frac{a}{(x+1)^{2}}+1$,
令h′(x)≤0,得a≥$\frac{(x+1)^{2}}{x}+(x+1)^{2}$=${x}^{2}+3x+\frac{1}{x}+3$对x∈(1,2]恒成立,
设m(x)=x2+3x+$\frac{1}{x}$+3,则m′(x)=2x+3-$\frac{1}{{x}^{2}}$,
∵1<x≤2,∴${m}^{'}(x)=2x+3-\frac{1}{{x}^{2}}$,
∵1<x≤2,∴${m}^{'}(x)=2x+3-\frac{1}{{x}^{2}}$>0,
∴m(x)在(1,2]上是增函数,
则当x=2时,m(x)有最大值为$\frac{27}{2}$,则a≥$\frac{27}{2}$,
当0<x≤1时,h(x)=-lnx+$\frac{a}{x+1}$+x,${h}^{'}(x)=-\frac{1}{x}-\frac{a}{(x+1)^{2}}+1$,
令h′(x)≤0,得a≥-$\frac{(x+1)^{2}}{x}$+(x+1)2=${x}^{2}+x-\frac{1}{x}-1$,
设t(x)=${x}^{2}+x-\frac{1}{x}-1$,
则${t}^{'}(x)=2x+1+\frac{1}{{x}^{2}}$>0,
∴t(x)在(0,1]上是增函数,∴t(x)≤t(1)=0,则a≥0.
综上所述:a的取值范围是[$\frac{27}{2},+∞$).
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质、构造法的合理运用.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈(0,+∞),sinx≥x | B. | ¬p:?x0∈(0,+∞),sinx0≥x0 | ||
| C. | ¬p:?x∈(-∞,0],sinx≥x | D. | ¬p:?x0∈(-∞,0],sinx0≥x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行于同一条直线的两条直线相互平行 | |
| B. | 平行于同一平面的两条直线相互平行 | |
| C. | 垂直于同一条直线的两条直线相互垂直 | |
| D. | 垂直于同一平面的两条直线相互垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
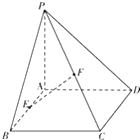 如图,已知PA⊥正方形ABCD所在平面,E、F分别是AB,PC的中点,二面角P-CD-A=45°.
如图,已知PA⊥正方形ABCD所在平面,E、F分别是AB,PC的中点,二面角P-CD-A=45°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com